题目内容
已知集合A={x∈R|kx2-4x+4=0}.
(1)若A=∅,求实数k的取值范围;
(2)若A中只有一个元素,求k的值及集合A.
(1)若A=∅,求实数k的取值范围;
(2)若A中只有一个元素,求k的值及集合A.
(1)A=∅,则kx2-4x+4=0无解.
若k=0,则方程等价为-4x+4=0,解得x=1,不满足条件.
若k≠0,则判别式△<0,即△=42-16k=16-16k<0,解得k>1.
综上k>1.
(2)若A中只有一个元素,
若k=0,则方程等价为-4x+4=0,解得x=1,满足条件.此时集合A={1}.
若k≠0,则判别式△=0,即16-16k=0,解得k=1.此时x=-
=
=2,集合A={2}.
所以k=0或k=1.
若k=0,则方程等价为-4x+4=0,解得x=1,不满足条件.
若k≠0,则判别式△<0,即△=42-16k=16-16k<0,解得k>1.
综上k>1.
(2)若A中只有一个元素,
若k=0,则方程等价为-4x+4=0,解得x=1,满足条件.此时集合A={1}.
若k≠0,则判别式△=0,即16-16k=0,解得k=1.此时x=-
| -4 |
| 2k |
| 4 |
| 2 |
所以k=0或k=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
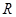 ,集合
,集合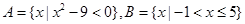 ,则
,则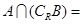 ( )
( )