题目内容
14.某几何体的三视图如图所示,则该三视图的体积为( )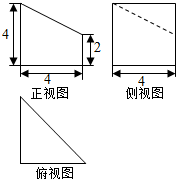
| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{80}{3}$ |
分析 由已知中的三视力可得该几何体是一个以俯视图为底面高为4的棱柱,截去一个以俯视图为底面高为2的棱锥,所得的组合体,进而得到答案.
解答 解:由已知中的三视力可得该几何体是一个棱柱,截去一个棱锥,所得的组合体,
棱柱和棱锥的底面均为俯视图,故底面面积S=$\frac{1}{2}$×4×4=8,
棱柱的高为4,棱锥的高为2,
故棱柱的体积为:4×8=32,
棱锥的体积为:$\frac{1}{3}$×8×2=$\frac{16}{3}$,
故组合体的体积V=32-$\frac{16}{3}$=$\frac{80}{3}$,
故选:D
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
5.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点F到渐近线和直线$x=\frac{a^2}{c}$的距离之比为2:1,则双曲线的渐近线方程为( )
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±2x |
2. 如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )
如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )
 如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )
如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )| A. | 150$\sqrt{2}$ | B. | 150$\sqrt{3}$ | C. | 300$\sqrt{2}$ | D. | 300$\sqrt{3}$ |
9.已知点P(-1,3,-4),且该点在三个坐标平面yOz平面,zOx平面、xOy平面上的射影的坐标依次为A、B、C,则以PA、PB、PC为棱的平行六面体体积为( )
| A. | 12 | B. | 6 | C. | 4 | D. | 以上结论都不对 |
19.已知函数f(x)=$\left\{\begin{array}{l}{(4a-3)x+5-4a(x<1)}\\{lo{g}_{a}(x-\frac{1}{2})(x≥1)}\end{array}\right.$是R上的减函数,那么a的取值范围是( )
| A. | (0,$\frac{\sqrt{2}}{2}$] | B. | (0,$\frac{3}{4}$] | C. | [$\frac{\sqrt{2}}{2}$,$\frac{3}{4}$] | D. | ($\frac{3}{4}$,1) |