题目内容
5.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点F到渐近线和直线$x=\frac{a^2}{c}$的距离之比为2:1,则双曲线的渐近线方程为( )| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±2x |
分析 利用已知条件求出双曲线的焦点坐标,列出方程得到ab的关系,然后求出双曲线的渐近线方程.
解答 解:由题意双曲线的渐近线方程为:y=±$\frac{b}{a}x$,F(c,0)到渐近线的距离为:$\frac{cb}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
到直线$x=\frac{a^2}{c}$的距离为:c-$\frac{{a}^{2}}{c}$=$\frac{{b}^{2}}{c}$,
双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点F到渐近线和直线$x=\frac{a^2}{c}$的距离之比为2:1,
可得:b:$\frac{{b}^{2}}{c}=2$,可得c=2b,∴a=$\sqrt{3}b$,
双曲线的渐近线方程为:y=$±\frac{\sqrt{3}}{3}x$.
故选:A.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
15.已知双曲线C:$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1的左右焦点分别为F1、F2,若双曲线C的右支上存在一点P,使得($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,O为坐标原点,且|$\overrightarrow{P{F}_{1}}$|=λ|$\overrightarrow{P{F}_{2}}$|,则实数λ等于( )
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
16.方程x-lg$\frac{1}{x}$-3=0的解所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
17.“m>1”是“函数f(x)=m+log2x(x≥1)不存在零点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
14.某几何体的三视图如图所示,则该三视图的体积为( )
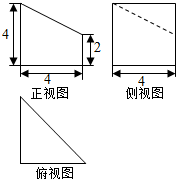

| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{80}{3}$ |