题目内容
6.某商场预计2018年第x月顾客对某种商品的需求量f(x)与x的关系近似满足:f(x)=-3x2+40x(x∈N*,1≤x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x(x∈N*,1≤x≤12),该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2018年第几月份销售该商品的月利润最大,最大月利润为多少元?分析 通过“利润=销售收入-成本”用x表示出利润,进而根据函数的单调性计算即得结论.
解答 解:利润y=[185-q(x)]f(x)
=[185-(150+2x)](-3x2+40x)
=6x3-185x2+1400x,
令y′=18x2-370x+1400=0,
解得:x=5或x=$\frac{140}{9}$,
又∵x∈N*,1≤x≤12,
∴x=5,
∴y在区间[1,5]上单调递增,在区间[5,12]上单调递减,
∴当x=5时,y取最大值6×53-185×52+1400×5=3125(元),
答:商场2018年第5月份销售该商品的月利润最大,最大月利润为3125元.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
16.方程x-lg$\frac{1}{x}$-3=0的解所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
17.“m>1”是“函数f(x)=m+log2x(x≥1)不存在零点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
14.某几何体的三视图如图所示,则该三视图的体积为( )
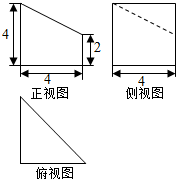

| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{80}{3}$ |
18.将函数y=cos2x的图象向右平移$\frac{π}{4}$个单位长度,得到函数y=f(x)•sin x的图象,则f(x)的表达式可以是( )
| A. | f(x)=-2cos x | B. | f(x)=2cos x | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin 2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin 2x+cos 2x) |
 如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.
如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.