题目内容
下列函数中,与函数f(x)=2x-1-
的奇偶性、单调性均相同的是( )
| 1 |
| 2x+1 |
| A.y=ex | B.y=ln(x+
| C.y=x2 | D.y=tanx |
∵f(x)=2x-1-
=
•2x-
•2-x=
(2x-2-x),x∈R;
∴f(-x)=
(2-x-2x)=-
(2x-2-x)=-f(x),
∴f(x)是奇函数;
又f′(x)=
(2xln2+2-xln2)>0,
∴f(x)是定义域上的增函数;
A中,y=ex是非奇非偶的函数,可以排除;
C中,y=x2是偶函数,可以排除;
D中,y=tanx在定义域{x|x≠
+kπ,k∈Z}上无单调性,可以排除;
故选:B.
| 1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(-x)=
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)是奇函数;
又f′(x)=
| 1 |
| 2 |
∴f(x)是定义域上的增函数;
A中,y=ex是非奇非偶的函数,可以排除;
C中,y=x2是偶函数,可以排除;
D中,y=tanx在定义域{x|x≠
| π |
| 2 |
故选:B.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
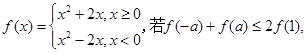 则实数
则实数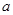 的取值范围是( )
的取值范围是( )