题目内容
【题目】某移动支付公司随机抽取了100名移动支付用户进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用移动支付超过3次的样本中,按性别用分层抽样随机抽取5名用户.
①求抽取的5名用户中男、女用户各多少人;
②从这5名用户中随机抽取2名用户,求抽取的2名用户均为男用户的概率.
(2)如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过0.05的前提下,认为“喜欢使用移动支付”与性别有关?
附表及公式: 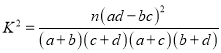
| 0.50 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【答案】(Ⅰ)①男用户有3人,女用户有2人.②![]() .(Ⅱ)见解析.
.(Ⅱ)见解析.
【解析】试题分析:(1)①由表格可知,样本中每周使用移动支付次数超过3次的男用户有45人,女用户30人, 按性别用分层抽样即可得到抽取的5名用户中男、女用户的人数;
②记抽取的3名男用户分别A,B,C;女用户分别记为d,e.根据古典概型的计算公式可得抽取的2名用户均为男用户的概率
(2)由图中表格可得![]() 列联表列联表中的数据代入公式
列联表列联表中的数据代入公式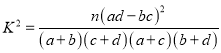 计算得出结果,作出判断即可.
计算得出结果,作出判断即可.
试题解析:
(1)①由表格可知,样本中每周使用移动支付次数超过3次的男用户有45人,女用户30人,
在这75人中,按性别用分层抽样的方法随机抽取5名用户,其中男用户有3人,女用户有2人.
②记抽取的3名男用户分别A,B,C;女用户分别记为d,e.
再从这5名用户随机抽取2名用户,共包含(A,B),(A,C),(A,d),(A,e),(B,C),(B,d),(B,e),
(C,d),(C,e),(d,e),10种等可能的结果
抽取的2名均为男用户这一事件包含(A,B) ,(A,C) ,(B,C)共计3种等可能的结果,
由古典概型的计算公式可得![]() .
.
(2)由图中表格可得列联表
不喜欢移动支付 | 喜欢移动支付 | 合计 | |
男 | 10 | 45 | 55 |
女 | 15 | 30 | 45 |
合计 | 25 | 75 | 100 |
将列联表中的数据代入公式计算得
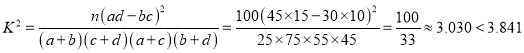 ,
,
所以,在犯错误概率不超过0.05的前提下,不能认为是否喜欢使用移动支付与性别有关.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案