题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 存在零点,且对任意
存在零点,且对任意![]() 都满足
都满足![]() ,若关于
,若关于![]() 的方程
的方程![]() (
(![]() )恰有三个不同的根,则实数
)恰有三个不同的根,则实数![]() 的取值范围是____.
的取值范围是____.
【答案】![]()
【解析】
令函数y=f(x)的零点为m,即f(m)=0,则由对任意m,n∈R都满足f[mf(m)+f(n)]=f2(m)+n.可得f[f(x)]=x,进而x的方程|f[f(x)]﹣3|=1﹣logax(a>0,a≠1)恰有三个不同的根,可转化为|x﹣3|=1﹣logax(a>0,a≠1)恰有三个不同的根,根据对数函数的图象和性质分类讨论后,可得答案.
令函数y=f(x)的零点为m,即f(m)=0,
∵对任意m,n∈R都满足f[mf(m)+f(n)]=f2(m)+n.
则f[f(n)]=n恒成立,
即f[f(x)]=x,
若关于x的方程|f[f(x)]﹣3|=1﹣logax(a>0,a≠1)恰有三个不同的根,
即|x﹣3|=1﹣logax(a>0,a≠1)恰有三个不同的根,
当0<a<1时,函数y=|x﹣3|与y=1﹣logax的图象如下图所示:
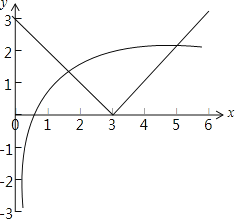
由图可知,函数y=|x﹣3|与y=1﹣logax的图象有两个交点,即关于x的方程|f[f(x)]﹣3|=1﹣logax(a>0,a≠1)恰有两个不同的根,不满足条件;
当1<a<3时,函数y=|x﹣3|与y=1﹣logax的图象如下图所示:
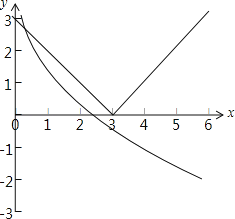
由图可知,函数y=|x﹣3|与y=1﹣logax的图象有一个交点,即关于x的方程|f[f(x)]﹣3|=1﹣logax(a>0,a≠1)恰有一个不同的根,不满足条件;
当a=3时,函数y=|x﹣3|与y=1﹣logax的图象如下图所示:

由图可知,函数y=|x﹣3|与y=1﹣logax的图象有两个交点,即关于x的方程|f[f(x)]﹣3|=1﹣logax(a>0,a≠1)恰有两个不同的根,不满足条件;
当a>3时,函数y=|x﹣3|与y=1﹣logax的图象如下图所示:
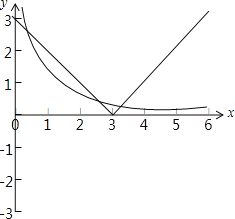
由图可知,函数y=|x﹣3|与y=1﹣logax的图象有三个交点,即关于x的方程|f[f(x)]﹣3|=1﹣logax(a>0,a≠1)恰有三个不同的根,满足条件;
综上所述,实数a的取值范围是(3,+∞),
故答案为:(3,+∞)

 寒假学与练系列答案
寒假学与练系列答案【题目】某移动支付公司随机抽取了100名移动支付用户进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用移动支付超过3次的样本中,按性别用分层抽样随机抽取5名用户.
①求抽取的5名用户中男、女用户各多少人;
②从这5名用户中随机抽取2名用户,求抽取的2名用户均为男用户的概率.
(2)如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过0.05的前提下,认为“喜欢使用移动支付”与性别有关?
附表及公式: 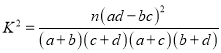
| 0.50 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |