题目内容
【题目】如图，已知
平面
平面
为等边三角形，
为
的中点.
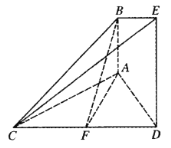
（1）求证：平面
平面
；
（2）求直线
和平面所成角的正弦值.
【答案】（1）见解析（2）
【解析】
（1）取CE的中点G，连接
，通过证明
平面
得面面垂直；
（2）过点B作
交
于M，连接FM，
即为所求线面角，根据线面位置关系计算正弦值.
（1）证明：取CE的中点G，连接.
∵F为CD的中点，∴
且
.
∵
平面
平面ACD，
∴
，∴
.
又
，∴
，
∴四边形
为平行四边形，则
.
∵
为等边三角形，F为CD的中点，∴
.
∵
平面
，
平面，∴
.
又
，故
平面.
∵
，∴平面.
∵
平面
，
∴平面
平面.
（2）不妨设
，过点B作交于M，
连接FM，由（1）平面平面，，
平面，
平面
平面
，所以
平面，
所以为所求线面角，
又因为平面
平面，所以
在
中，
，
在直角梯形
中，
，所以
为等腰三角形，
，
所以直线
和平面所成角的正弦值为.
【题目】3月12日，全国政协总工会界别小组会议上，人社部副部长汤涛在回应委员呼声时表示无论是从养老金方面，还是从人力资源的合理配置来说，延迟退休是大势所趋.不过，汤部长也表示，不少职工对于延迟退休有着不同的意见.某高校一社团就是否同意延迟退休的情况随机采访了200名市民，并进行了统计，得到如下的
列联表：
赞同延迟退休 | 不赞同延迟退休 | 合计 | |
男性 | 80 | 20 | 100 |
女性 | 60 | 40 | 100 |
合计 | 140 | 60 | 200 |
（1）根据上面的列联表判断能否有
的把握认为对延迟退休的态度与性别有关；
（2）为了进一步征求对延迟退休的意见和建议，从抽取的200位市民中对不赞同的按照分层抽样的方法抽取6人，再从这6人中随机抽出3名进行电话回访，求3人中至少有1人为男性的概率.
附：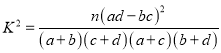 
，其中
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】《中华人民共和国道路交通安全法》第47条的相关规定：机动车行经人行道时，应当减速慢行；遇行人正在通过人行道，应当停车让行，俗称“礼让斑马线”， 《中华人民共和国道路交通安全法》第90条规定：对不礼让行人的驾驶员处以扣3分，罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据：
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
（1）请利用所给数据求违章人数
与月份
之间的回归直线方程
；
（2）预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式：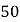 
， 
.
参考数据： 
.
【题目】某移动支付公司随机抽取了100名移动支付用户进行调查，得到如下数据：
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
（1）在每周使用移动支付超过3次的样本中，按性别用分层抽样随机抽取5名用户.
①求抽取的5名用户中男、女用户各多少人；
②从这5名用户中随机抽取2名用户，求抽取的2名用户均为男用户的概率.
（2）如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”，能否在犯错误概率不超过0.05的前提下，认为“喜欢使用移动支付”与性别有关？
附表及公式：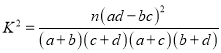 
| 0.50 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
