题目内容
已知关于x的不等式:|2x-m|≤1的整数解有且仅有一个值为2.则整数m的值为 ;
4
解:由关于x的不等式:|2x-m|≤1 可得-1≤2x-m≤1,解得 m-1 /2 ≤x≤m+1 /2 .
由于整数解有且仅有一个值为2,
∴
1<(m-1)/ 2 <2
2<(m+1) /2 <3 ,
即
3<m<5
3<m<5 ,故 m=4,
故答案为 4
由于整数解有且仅有一个值为2,
∴
1<(m-1)/ 2 <2
2<(m+1) /2 <3 ,
即
3<m<5
3<m<5 ,故 m=4,
故答案为 4

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 的解集为( )
的解集为( )


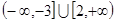
 ,函数
,函数 .
. 时,求使
时,求使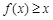 成立的
成立的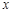 的集合;
的集合; 在区间
在区间 上的最小值.
上的最小值.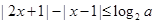 (其中
(其中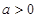 )。
)。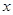 使
使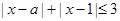 成立,则实数
成立,则实数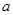 的取值范围是
的取值范围是  ,
,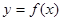 的图像;(2)解不等式
的图像;(2)解不等式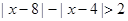 。
。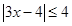 的解集是
的解集是 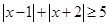 的解集为( )
的解集为( )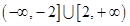
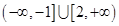
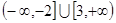

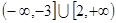
 恒成立, 则
恒成立, 则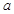 的取值范围是 。
的取值范围是 。