题目内容
1．设f（x）=$\left\{\begin{array}{l}{{x}^{2}，x∈[0，1]}\\{\frac{1}{x}，x∈（1，e]}\end{array}\right.$（其中e为自然对数的底数），则y=f（x）的图象与x=0，x=e以及x轴所围成图形的面积为$\frac{4}{3}$．分析 由题意，画出图形，利用定积分表示围成图形的面积，然后计算即可．
解答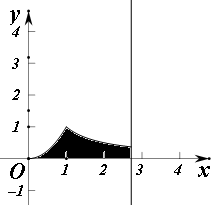 
解：y=f（x）的图象与x=0，x=e以及x轴所围成图形如图，面积为${∫}_{0}^{1}{x}^{2}dx+{∫}_{1}^{e}\frac{1}{x}dx$=$\frac{1}{3}{x}^{3}{|}_{0}^{1}+lnx{|}_{1}^{e}$=$\frac{4}{3}$；
故答案为：$\frac{4}{3}$．
点评 本题考查了利用定积分求封闭图形的面积；关键是利用定积分正确表示面积，然后再去计算定积分．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．已知在四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{DC}$=（1，1），$\frac{1}{|\overrightarrow{BA}|}$$\overrightarrow{BA}$+$\frac{1}{|\overrightarrow{BC}|}$$\overrightarrow{BC}$=$\frac{3}{2|\overrightarrow{BD}|}$$\overrightarrow{BD}$，则四边形ABCD的面积为（ ）
| A． | $\frac{\sqrt{13}}{8}$ | B． | $\frac{3\sqrt{5}}{2}$ | C． | $\frac{4\sqrt{26}}{3}$ | D． | $\frac{3\sqrt{7}}{4}$ |