题目内容
【题目】在数列{an}中，a1=1，3anan﹣1+an﹣an﹣1=0（n≥2）．
（1）求证：数列{ 
}等差数列；
（2）数列bn=anan+1 ， 求数列bn的前n项和．
【答案】
（1）解：因为3anan﹣1+an﹣an﹣1=0（n≥2），
整数，得 
﹣ 
=3（n≥2），
所以数列{ }是以1为首项，3为公差的等差数列
（2）解：由（1）可得 =1+3（n﹣1）=3n﹣2，
所以an= 
. 
= 
【解析】（1）利用3anan﹣1+an﹣an﹣1=0（n≥2），转化为： 
﹣ =3（n≥2）即可证明数列{ }是等差数列．（2）求出an ， 推出bn ， 利用裂项法求解数列的和即可．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系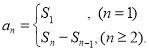
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
名校课堂系列答案
相关题目
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度，随机选取了140位市民进行调查，调查结果统计如下：
支持 | 不支持 | 总计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
（I）根据已知数据，把表格数据填写完整；
（II）利用（1）完成的表格数据回答下列问题：
（ⅰ）能否在犯错误的概率不超过0.001的前提下认为性别与支持申办足球世界杯有关；
（ⅱ）已知在被调查的支持申办足球世界杯的男性市民中有5位退休老人，其中2位是教师，现从这5位退休老人中随机抽取3人，求至多有1位老师的概率。
附：
，其中
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
