题目内容

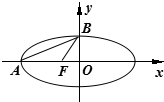
椭圆焦点在x轴上，A为该椭圆右顶点，P在椭圆上一点，∠OPA=90°，则该椭圆的离心率e的范围是（　　）
A．[
1
2
，1）		B．（
2
2
，1）		C．[
1
2
，
6
3
）		D．（0，
2
2
）
可设椭圆的标准方程为：
x2
a2
+
y2
b2
=1（a＞b＞0）．
设P（x，y），∵∠OPA=90°，∴点P在以OA为直径的圆上．
该圆为：(x-
a
2
)2+y2=(
a
2
)2，化为x2-ax+y2=0．
联立
x2-ax+y2=0
x2
a2
+
y2
b2
=1
化为（b2-a2）x2+a3x-a2b2=0，
则ax=
-a2b2
b2-a2
，解得x=
ab2
c2
，
∵0＜x＜a，∴0＜
ab2
c2
＜a，
化为c2＞b2=a2-c2，
∴e2＞
1
2
，又1＞e＞0．
解得
2
2
＜e＜1．
∴该椭圆的离心率e的范围是(
2
2
，1)．
故选：C．
练习册系列答案
相关题目
如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左顶点为A，左焦点为F，上顶点为B，若∠BAO+∠BFO=90°，则该椭圆的离心率是______．
已知定点N（0，1），动点A，B分别在抛物线y=
1
4
x2及曲线
x2
3
+
y2
4
=1(x＜0，y＞0)上，若B在A的上方，且AB∥y轴，则△ABN的周长l的取值范围是（　　）
A．（
2
3
，2）		B．（
5
2
，
9
2
）		C．（
10
3
，4）		D．（
5
3
，3）
椭圆
x2
5
+
y2
4
=1的焦距是（　　）
A．1B．2C．4D．8
椭圆x2+2y2=6的离心率为（　　）
A．
2
B．
2
2
C．
1
2
D．
3
3
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的短轴长为4，F1F2分别是椭圆C的左，右焦点，直线y=x与椭圆C在第一象限内的交点为A，△AF1F2的面积为2
6
，点P（x0，y0），是椭圆C上的动点w．
（1）求椭圆C的方程；
（2）若∠F1PF2为钝角，求点P的横坐标x0的取值范围；
（3）求
3
PF1+
2
PA的最小值．
已知F1是椭圆
x2
25
+
y2
9
=1的左焦点，P是椭圆上的动点，A（1，1）是一定点，则PA+PF1的最大值为______．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0），c=
a2-b2
，圆（x-c）2+y2=c2与椭圆恰有两个公共点，则椭圆的离心率e的取值范围是______．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)中，有c＞b，则离心率e的取值范围是（　　）
A．(0，
2
2
)		B．(
2
2
，1)		C．（0，1）D．(1，
2
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网