题目内容
(本小题满分12分)已知函数f(x)=ln(x+1)-x.
⑴求函数f(x)的单调递减区间;
⑵若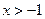 ,证明:
,证明: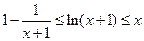 .
.
⑴求函数f(x)的单调递减区间;
⑵若
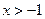 ,证明:
,证明: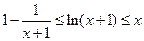 .
.解:⑴函数f(x)的定义域为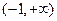 .
.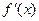 =
=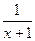 -1=-
-1=-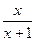 。由
。由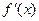 <0及x>-1,得x>0.∴当x∈(0,+∞)时,f(x)是减函数,即f(x)的单调递减区间为(0,+∞).
<0及x>-1,得x>0.∴当x∈(0,+∞)时,f(x)是减函数,即f(x)的单调递减区间为(0,+∞).
⑵证明:由⑴知,当x∈(-1,0)时,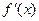 >0,当x∈(0,+∞)时,
>0,当x∈(0,+∞)时,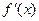 <0,
<0,
因此,当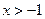 时,
时,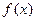 ≤
≤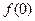 ,即
,即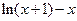 ≤0∴
≤0∴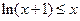 .
.
令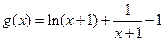 ,则
,则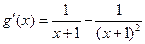 =
=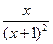 .
.
∴当x∈(-1,0)时, <0,当x∈(0,+∞)时,
<0,当x∈(0,+∞)时, >0.
>0.
∴当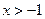 时,
时,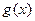 ≥
≥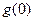 ,即
,即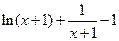 ≥0,∴
≥0,∴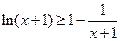 .
.
综上可知,当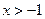 时,有
时,有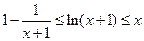 .
.
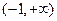 .
.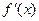 =
=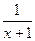 -1=-
-1=-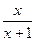 。由
。由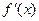 <0及x>-1,得x>0.∴当x∈(0,+∞)时,f(x)是减函数,即f(x)的单调递减区间为(0,+∞).
<0及x>-1,得x>0.∴当x∈(0,+∞)时,f(x)是减函数,即f(x)的单调递减区间为(0,+∞).⑵证明:由⑴知,当x∈(-1,0)时,
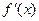 >0,当x∈(0,+∞)时,
>0,当x∈(0,+∞)时,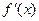 <0,
<0,因此,当
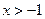 时,
时,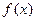 ≤
≤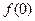 ,即
,即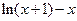 ≤0∴
≤0∴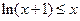 .
.令
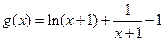 ,则
,则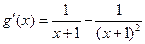 =
=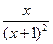 .
.∴当x∈(-1,0)时,
 <0,当x∈(0,+∞)时,
<0,当x∈(0,+∞)时, >0.
>0.∴当
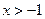 时,
时,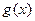 ≥
≥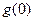 ,即
,即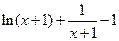 ≥0,∴
≥0,∴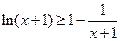 .
.综上可知,当
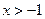 时,有
时,有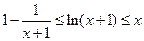 .
.略

练习册系列答案
相关题目
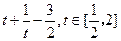
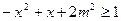 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.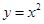 在点P处的切线的倾斜角为
在点P处的切线的倾斜角为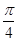 ,则P点坐标为 ( )
,则P点坐标为 ( )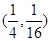
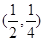
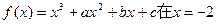 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线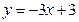 在点(1,0)处相切,求a、b
在点(1,0)处相切,求a、b 、c的值.
、c的值. 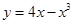 在点(-1,-3)处的切线方程是 ( )
在点(-1,-3)处的切线方程是 ( )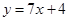 B
B 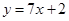 C
C 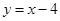 D
D 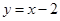
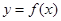 的导函数
的导函数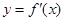 的图象,下列说法错误的是…………( )
的图象,下列说法错误的是…………( )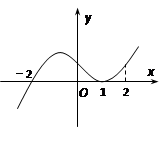
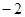 是函数
是函数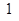 是函数
是函数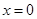 处切线的斜率大于零;
处切线的斜率大于零;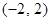 上单调递增.
上单调递增.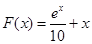 的作用,(x 的单位:m, F的单位:N),则它从
的作用,(x 的单位:m, F的单位:N),则它从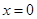 运动到
运动到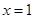 时
时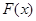 所做的功等于 J。
所做的功等于 J。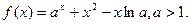
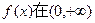 上单调递增;
上单调递增;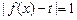 有三个不同的实根,求t的值;
有三个不同的实根,求t的值; 的取值范围。
的取值范围。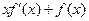 ≤0,对任意的正数a,b,若a<b,则必有 ( ▲ )
≤0,对任意的正数a,b,若a<b,则必有 ( ▲ )