题目内容
(本小题满分12分)
已知函数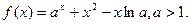
(I)求证:函数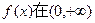 上单调递增;
上单调递增;
(II)若方程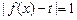 有三个不同的实根,求t的值;
有三个不同的实根,求t的值;
(III)对 的取值范围。
的取值范围。
已知函数
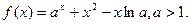
(I)求证:函数
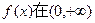 上单调递增;
上单调递增;(II)若方程
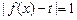 有三个不同的实根,求t的值;
有三个不同的实根,求t的值;(III)对
 的取值范围。
的取值范围。解:(I)
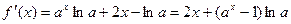 …………2分
…………2分由于
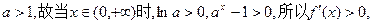
故函数
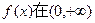 上单调递增。 …………4分
上单调递增。 …………4分(II)令
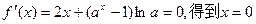 …………5分
…………5分 的变化情况表如下:
的变化情况表如下: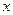 | 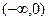 | 0 | 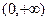 |
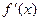 | — | 0 | + |
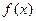 |  | 极小值 |  |
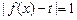 有三个不同的实根,
有三个不同的实根,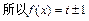 有三个根,
有三个根,又因为当
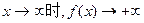 ,
,所以
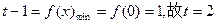 …………8分
…………8分(III)由(II)可知
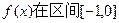 上单调递减,在区间[0,1]上单调递增。
上单调递减,在区间[0,1]上单调递增。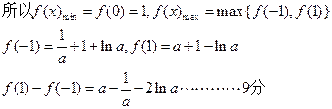
记
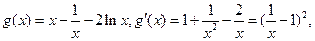
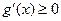 (当x=1时取等号)
(当x=1时取等号)所以
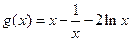 递增
递增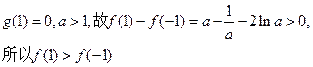
于是
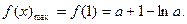 ………………11分
………………11分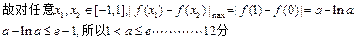
(文科)(第(1)小题6分,第(2)小题6分)
(1)
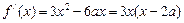 , …………2分
, …………2分由
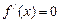 得
得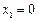 ,
,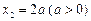 . …………3分
. …………3分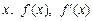 的变化情况表如下:
的变化情况表如下: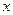 | 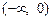 | 0 | 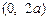 | 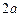 | 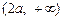 |
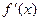 | + | 0 | — | 0 | + |
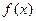 |  | 极大值 |  | 极小值 |  |
 的增区间为:
的增区间为: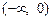 、
、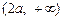 ,减区间为:
,减区间为: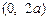 . …………6分
. …………6分(2)由(1)可知,只有
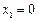 、
、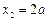 处切线都恰好与
处切线都恰好与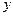 轴垂直,
轴垂直,∴
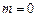 ,
,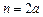 ,
, ,
,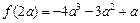 . …………8分
. …………8分由曲线
 在区间
在区间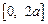 上与
上与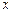 轴相交,可得:
轴相交,可得: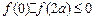 , …………9分
, …………9分∵
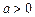 ∴
∴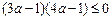 . …………10分
. …………10分解得
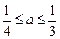 ,
,∴实数
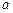 的取值范围是
的取值范围是 . …………12分
. …………12分略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
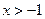 ,证明:
,证明: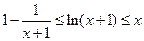 .
.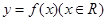 上任一点
上任一点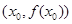 处的切线斜率
处的切线斜率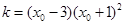 ,则该函数的单调递减区间为
,则该函数的单调递减区间为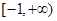
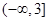
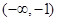
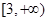
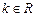 ,函数
,函数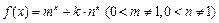 .
.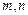 满足
满足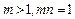 ,函数
,函数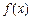 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的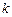
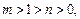 判断函数
判断函数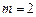 ,
,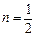 ,且
,且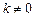 ,求函数
,求函数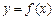 的对称轴或对称中心.
的对称轴或对称中心.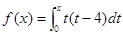 在
在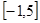 上( )
上( )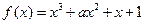 ,(
,(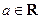 )
)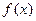 的单调区间;
的单调区间;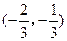 内是减函数,求
内是减函数,求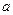 的取值范围.
的取值范围.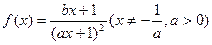 ,且
,且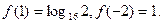
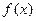 的表达式;
的表达式;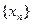 的项满足
的项满足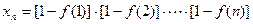 ,试求
,试求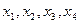 ;
;
 的单调性;
的单调性; 的最大值和最小值.
的最大值和最小值. ,那么这个三角形顶角的正弦值 ( )
,那么这个三角形顶角的正弦值 ( )