题目内容
已知函数f(t)=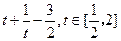
(1)求f(t)的值域G;
(2)若对于G内的所有实数x,不等式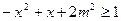 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
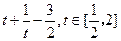
(1)求f(t)的值域G;
(2)若对于G内的所有实数x,不等式
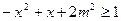 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.解:(1)∵t>0, ∴ 当且仅当t=1时,取等号,∴f(t)≥
当且仅当t=1时,取等号,∴f(t)≥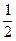 ,………(2分)
,………(2分)
设 时,
时,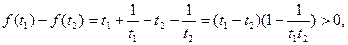 所以f(t)
所以f(t)
在t∈[ ]上是单调递减的,同理可证f(t) 在t∈[
]上是单调递减的,同理可证f(t) 在t∈[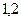 ]上是单调递增的………(4分)
]上是单调递增的………(4分)
又 ,即
,即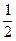 ≤f(t)≤1
≤f(t)≤1
∴f(t)的值域G为[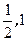 ] ………………………………………………………(6分)
] ………………………………………………………(6分)
(2)由题知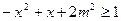 在x∈[
在x∈[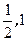 ]上恒成立
]上恒成立
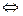
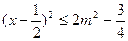 在x∈[
在x∈[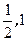 ]上恒成立.…………………………………(7分)
]上恒成立.…………………………………(7分)
当x∈[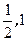 ]时 .
]时 .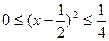 ………………………………………(9分)
………………………………………(9分)

解得m≥ 或m≤
或m≤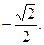 …………………………………………………(11分)
…………………………………………………(11分)
实数m的取值范围是(-∞, ]∪[
]∪[ ,+∞).……………………………(12分)
,+∞).……………………………(12分)
 当且仅当t=1时,取等号,∴f(t)≥
当且仅当t=1时,取等号,∴f(t)≥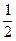 ,………(2分)
,………(2分)设
 时,
时,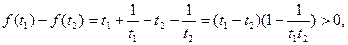 所以f(t)
所以f(t) 在t∈[
 ]上是单调递减的,同理可证f(t) 在t∈[
]上是单调递减的,同理可证f(t) 在t∈[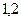 ]上是单调递增的………(4分)
]上是单调递增的………(4分)又
 ,即
,即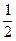 ≤f(t)≤1
≤f(t)≤1∴f(t)的值域G为[
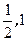 ] ………………………………………………………(6分)
] ………………………………………………………(6分)(2)由题知
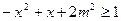 在x∈[
在x∈[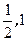 ]上恒成立
]上恒成立
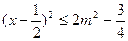 在x∈[
在x∈[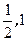 ]上恒成立.…………………………………(7分)
]上恒成立.…………………………………(7分)当x∈[
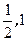 ]时 .
]时 .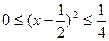 ………………………………………(9分)
………………………………………(9分)
解得m≥
 或m≤
或m≤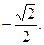 …………………………………………………(11分)
…………………………………………………(11分)实数m的取值范围是(-∞,
 ]∪[
]∪[ ,+∞).……………………………(12分)
,+∞).……………………………(12分)略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
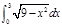 表示 ( )
表示 ( )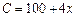 ,月最高产量为150台,出厂单价p(单位:万元)与月产量x的函数关系为
,月最高产量为150台,出厂单价p(单位:万元)与月产量x的函数关系为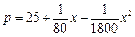 .
.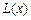 ;
;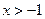 ,证明:
,证明: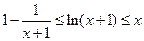 .
.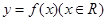 上任一点
上任一点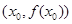 处的切线斜率
处的切线斜率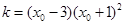 ,则该函数的单调递减区间为
,则该函数的单调递减区间为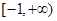
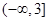
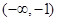
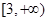
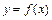 的图象如图所示,则该函数的导函数的图象是
的图象如图所示,则该函数的导函数的图象是 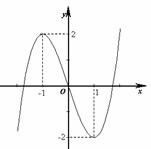
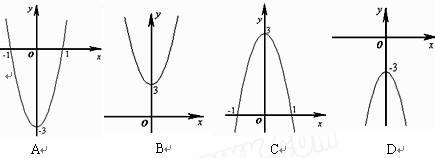
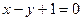
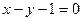
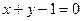
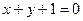
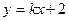 与曲线
与曲线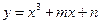 相切于点
相切于点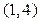 ,则
,则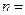 .
.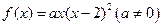 有极大值
有极大值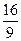 ,则
,则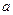 等于
等于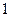

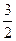
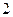 (
(
