题目内容
16．光线沿直线L1：3x-4y+4=0方向射向直线L：y=2x+1并反射回来，求反射光线所在的直线方程．分析 由入射角等于反射角，利用来角公式先求出反射光线的斜率，再由反射光线经过光线沿直线L1：3x-4y+4=0方向射向直线L：y=2x+1的交点，能求出反射光线所在的直线方程．
解答 解：∵光线沿直线L1：3x-4y+4=0方向射向直线L：y=2x+1并反射回来，
∴法线垂直于直线L：y=2x+1，∴法线的斜率k′=-$\frac{1}{2}$，
设反射光线的斜率为k，
∵光线沿直线L1：3x-4y+4=0方向射向直线L：y=2x+1并反射回来，
∴入射光线的斜率${k}_{1}=\frac{3}{4}$，
∵入射角等于反射角，∴|$\frac{k-（-\frac{1}{2}）}{1+（-\frac{1}{2}）k}$|=|$\frac{\frac{3}{4}-（-\frac{1}{2}）}{1+\frac{3}{4}×（-\frac{1}{2}）}$|，
解得k不存在或k=$\frac{3}{4}$（舍），
∵反射光线经过光线沿直线L1：3x-4y+4=0方向射向直线L：y=2x+1的交点M，
解方程组$\left\{\begin{array}{l}{3x-4y+4=0}\\{y=2x+1}\end{array}\right.$，得M（0，1），
∴反射光线所在的直线方程为y=0．
点评 本题考查直线方程的求法，是中档题，解题时要认真审题，注意夹角公式、直线方程、入射直线与反射直线的关系等知识点的合理运用．
练习册系列答案
相关题目
如图，在正方体ABCD-A1B1C1D1中，M，N分别是CD，CC1的中点，给出下列命题：
11．
如图，侧棱垂直于底面的三棱柱ABC-A1B1C1的六个顶点都在一个半球面上，且AB=AC，B1C1=$\sqrt{2}$BB1，则异面直线AC1与A1B所成的角为（ ）
如图，侧棱垂直于底面的三棱柱ABC-A1B1C1的六个顶点都在一个半球面上，且AB=AC，B1C1=$\sqrt{2}$BB1，则异面直线AC1与A1B所成的角为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
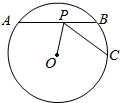如图，点P为⊙O的弦AB上一点，且AP=9，BP=4，连接OP，作PC⊥OP交圆于C，则PC的长为（ ）