��Ŀ����
����Ŀ����ͼ��ʾ�ľ�Ҷͼ��¼�˼ס��������5��ͬѧ��Ͷ�����д����������¼����һ������ģ������ȷ�ϣ���ͼ����![]() ��ʾ.
��ʾ.
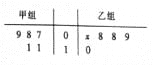
��1��������ͬѧͶ�����д�����ƽ�����ȼ���ͬѧ��ƽ������1����![]() ������ͬѧͶ�����д����ķ��
������ͬѧͶ�����д����ķ��
��2���ڣ�1���������£��ֱ�Ӽס�������Ͷ�����д�������10�ε�ͬѧ�У������ѡȡһ������������ͬѧ��Ͷ�����д���֮��Ϊ16�ĸ���.
���𰸡���1��![]() ��
�� ![]() ����2��
����2��![]() .
.
�������������������1����ƽ�����ĸ���ɽ��![]() ��ֵ���ɷ���ĸ�������Ͷ�����д����ķ����2���Ӽס�������Ͷ�����д�������
��ֵ���ɷ���ĸ�������Ͷ�����д����ķ����2���Ӽס�������Ͷ�����д�������![]() �ε�ͬѧ�У������ѡȡһ������
�ε�ͬѧ�У������ѡȡһ������![]() �֣�Ͷ�����д���֮��Ϊ
�֣�Ͷ�����д���֮��Ϊ![]() ����
����![]() �֣��ʿ���������.
�֣��ʿ���������.
�����������1��������ã� ![]() �����
�����![]() ��
�� ![]() ��
��
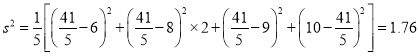 .
.
��2���Ǽ���Ͷ�����д�������10�ε�ͬѧΪ![]() �����ǵ����д����ֱ�Ϊ9��8��7.
�����ǵ����д����ֱ�Ϊ9��8��7.
����Ͷ�����д�������10�ε�ͬѧΪ![]() �����ǵ����д����ֱ�Ϊ6��8��8��9.
�����ǵ����д����ֱ�Ϊ6��8��8��9.
�����⣬��ͬ��ѡȡ�����У� ![]()
��12��.
����������ͬѧ��Ͷ�����д���֮��Ϊ16��Ϊ�¼�������ǡ����![]() ��3��.
��3��.
![]() .
.

����Ŀ��2013�꣬������������59����������������һ���£��������ͳ�ƣ������д�1��1����1��30�յ�30������26�����������������������������ָ��(AQI)�����涨(����)������������ָ����Ϊ���������У��ж���Ⱦ(�ļ�)ָ��Ϊ151��200���ض���Ⱦ(�弶)ָ��Ϊ201��300��������Ⱦ(����)ָ������300.�����1��ij�۲���¼��4����AQIָ��M�뵱��Ŀ���ˮƽ�ɼ���y(ǧ��)���������2��ij����۲���¼�ı���1��1�յ�1��30��AQIָ��Ƶ����ͳ�ƽ����
��1��
AQIָ��M | 900 | 700 | 300 | 100 |
�����ɼ���y/ǧ�� | 0.5 | 3.5 | 6.5 | 9.5 |
��2��
AQIָ�� | [0��200] | (200��400] | (400��600] | (600��800] | (800��1000] |
Ƶ�� | 3 | 6 | 12 | 6 | 3 |
(1)�����x��![]() �����ݱ�1�����ݣ����y����x�����Իع鷽�̣�
�����ݱ�1�����ݣ����y����x�����Իع鷽�̣�
(2)���ݱ�2������30��AQIָ����ƽ��ֵ��

