题目内容
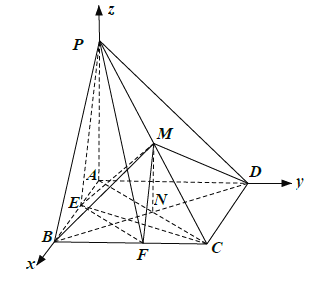
【题目】如图,在四棱锥![]() 中,底而
中,底而![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 上的动点(
上的动点(![]() ,
,![]() 与所在棱的端点不重合),且满足
与所在棱的端点不重合),且满足![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值
的余弦值
【答案】(1)见解析;(2)![]()
【解析】
(1)连结![]() 交
交![]() 于
于![]() 连结
连结![]() ,则
,则![]() ,
,![]() 面
面![]() ,
,![]() ,而
,而![]() ,
,![]() 面
面![]() ,易证
,易证![]() ,则
,则![]() 面
面![]() ,可得平面
,可得平面![]() 平面
平面![]() .解法二:通过建立空间直角坐标系,找出平面
.解法二:通过建立空间直角坐标系,找出平面![]() 平面
平面![]() 的法向量,通过法向量互相垂直来证明.
的法向量,通过法向量互相垂直来证明.
(2)通过建立空间直角坐标系,找到两个平面法向量之间的夹角余弦,从而得到二面角的余弦值.
(1)【解法一】:(综合法)
证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
因为底面![]() 为正方形,所以
为正方形,所以![]() ,
,![]() ,
,
又因为![]() ,所以
,所以![]() .
.
由![]() 底面
底面![]() 知,
知,![]() 底面
底面![]() ,
,
又![]() 底面
底面![]() ,所以
,所以![]() ;
;
又![]() ;
;![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
在![]() 中,因为
中,因为![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
【解法二】
(向量法)
因为![]() 底面
底面![]() ,
,![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系
轴正方向,建立如图所示的空间直角坐标系![]() .则
.则
![]() ,
,![]() ,
,![]() ,
,![]() .设
.设![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
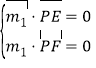 即
即![]() 可取
可取![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
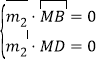 即
即![]() 可取
可取![]() .
.
因为![]() ,所以
,所以![]() .
.
所以平面![]() 平面
平面![]() .
.
(2)解:设![]() ,
,
由题意知,![]() ,又
,又![]() ,
,
所以![]() .
.
易知当三棱锥![]() 的体积最大时,
的体积最大时,![]() ,即此时
,即此时![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点.
的中点.
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系
轴正方向,建立如图所示的空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
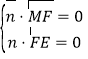 即
即![]() 可取
可取![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
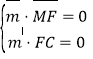 即
即![]() 可取
可取![]() .
.
则![]() .
.
由图知所求二面角为钝二面角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案【题目】某地区为了调查高粱的高度、粒的颜色与产量的关系,对700棵高粱进行抽样调查,得到高度频数分布表如下:
表1:红粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频 数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:白粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频 数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)估计这700棵高粱中红粒高粱的棵数;
(2)估计这700棵高粱中高粱高(![]() )在
)在![]() 的概率;
的概率;
(3)在样本的红粒高粱中,从高度(单位:![]() )在
)在![]() 中任选3棵,设
中任选3棵,设![]() 表示所选3棵中高(单位:
表示所选3棵中高(单位:![]() )在
)在![]() 的棵数,求
的棵数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.