题目内容
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() , 如图(2).
, 如图(2).

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出![]() ,
,![]() ,从而
,从而![]() 面
面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;
;
(2)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,则
,则![]() 面
面![]() ,以
,以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,利用向量法能求出平面
轴建立空间直角坐标系,利用向量法能求出平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)证明:![]() 四边形
四边形![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的两个三等分点,
的两个三等分点,
![]() 四边形
四边形![]() 是正方形,
是正方形,![]()
![]() ,
,
![]()
![]() ,且
,且![]() ,
,![]()
![]() 面
面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,则
,则![]() 面
面![]() ,
,
以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,如图所示:
轴建立空间直角坐标系,如图所示:

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则 ,∴
,∴ ,取
,取![]() ,得:
,得:![]() ,
,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,
,
则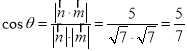 .
.
![]() 平面
平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.


