题目内容
2．方程${x^2}+{y^2}+ax-2ay+a+\frac{1}{4}=0$为圆的方程，则a的范围为$（-∞，-\frac{1}{5}）∪（1，+∞）$．分析 利用二元二次方程表示圆的充要条件，列出方程求解即可．
解答 解：方程${x^2}+{y^2}+ax-2ay+a+\frac{1}{4}=0$为圆的方程，
则：a2+（-2a）2-4（a+$\frac{1}{4}$）＞0，即5a2-4a-1＞0，
解得a∈$（-∞，-\frac{1}{5}）∪（1，+∞）$
故答案为：$（-∞，-\frac{1}{5}）∪（1，+∞）$．
点评 本题考查圆的方程的应用，二元二次方程表示圆的体积的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
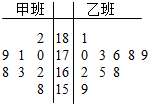随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图示，根据茎叶图解答下列问题；