题目内容
17.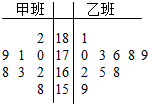 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图示,根据茎叶图解答下列问题;
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图示,根据茎叶图解答下列问题;(1)计算甲班与乙班的身高数据的中位数.
(2)判断哪个班的平均身高较高.
分析 本题中“茎是百位和十位”,叶是个位,从图中分析出参与运算的数据,代入相应公式即可解答
解答 解:(1)甲班的中位数为$\frac{170+168}{2}=169$,乙班的中位数为$\frac{170+173}{2}=171.5$…(7分)
(2)甲班平均身高为$\frac{1}{10}(182+170×4+19+160×4+21+158)$=170cm.
乙班平均身高为$\frac{1}{10}(181+170×5+26+160×3+18+159)$=171.4cm.乙班身高较高…(14分).
点评 茎叶图的茎是高位,叶是低位,所以本题中“茎是百位和十位”,叶是个位,从图中分析出参与运算的数据,代入相应公式即可解答.从茎叶图中提取数据是利用茎叶图解决问题的关键.

练习册系列答案
相关题目
7.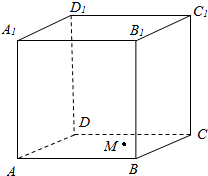 如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
 如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
8.已知函数f(x)的定义域是R,f′(x)是f(x)的导数,f(1)=e,g(x)=f′(x)-f(x),g(1)=0,g(x)的导数恒大于零,函数h(x)=f(x)-ex(e=2.71828…是自然对数的底数)的最小值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
6.某化工厂生产一种化工产品,据负责该产品生产的部门预算,当该产品年产量在50吨至300吨之间时,其生产的总成本y(万元)与年产量x(吨)之间的部分对应数据大致如下表:
(1)给出如下四个函数:
①y=ax2+b,②y=$\frac{1}{10}{x}^{2}+ax+b$,③y=a•bx,④y=a•logbx.根据上表数据,从上述四个函数中选取一个最恰当的函数描述y与x的变化关系,并通过表中前两组数据,求出y与x的函数解析式;
(2)根据你求出的函数解析式,试问当年产量为多少吨时,生产每吨的平均成本最低?每吨的最低成本是多少?
(3)若将每吨产品的出厂价定为16万元,则年产量为多少吨时,方可使得全年的利润最大?并求出全年的最大利润.
| 生产量x(单位:吨) | 50 | 100 | 130 | 180 | 200 | 250 | 300 |
| 生产总成本y(单位:万元) | 2750 | 2000 | 1750 | 1800 | 2050 | 2750 | 4050 |
①y=ax2+b,②y=$\frac{1}{10}{x}^{2}+ax+b$,③y=a•bx,④y=a•logbx.根据上表数据,从上述四个函数中选取一个最恰当的函数描述y与x的变化关系,并通过表中前两组数据,求出y与x的函数解析式;
(2)根据你求出的函数解析式,试问当年产量为多少吨时,生产每吨的平均成本最低?每吨的最低成本是多少?
(3)若将每吨产品的出厂价定为16万元,则年产量为多少吨时,方可使得全年的利润最大?并求出全年的最大利润.
7. 读程序
读程序
对甲乙两程序和输出结果判断正确的是( )
 读程序
读程序对甲乙两程序和输出结果判断正确的是( )
| A. | 程序不同,结果不同 | B. | 程序相同,结果不同 | ||
| C. | 程序不同,结果相同 | D. | 程序相同,结果相同 |
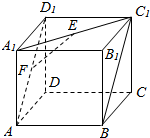 如图所示,已知正方体ABCD-A1B1C1D1,E、F分别是正方形A1B1C1D1和ADD1A1的中心,求EF和CD所成的角.
如图所示,已知正方体ABCD-A1B1C1D1,E、F分别是正方形A1B1C1D1和ADD1A1的中心,求EF和CD所成的角.