题目内容
12.已知函数f(x)=3x3+ax+1(a为常数)f(5)=7,则f(-5)=-5.分析 由已知中函数f(x)=3x3+ax+1,可得f(5)+f(-5)=2,进而得到答案.
解答 解:∵函数f(x)=3x3+ax+1,
∴f(5)+f(-5)=2,
又∵f(5)=7,
∴f(-5)=-5,
故答案为:-5
点评 本题考查的知识点是函数奇偶性的性质,根据已知得到f(5)+f(-5)=2,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.一个空间简单几何体的正视图是圆,则该几何体不可能是( )
| A. | 圆柱 | B. | 三棱柱 | C. | 球 | D. | 圆锥 |
7.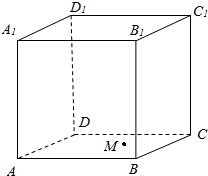 如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
 如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
1.cos24°cos36°-sin24°cos54°=( )
| A. | cos12° | B. | sin12° | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |