Question

【题目】ABC的三个角A，B，C所对的边分别是a，b，c，向量=(2，－1)，=(sinBsinC，+2cosBcosC)，且⊥.

（1）求角A的大小；

（2）现给出以下三个条件：①B=45；②2sinC-(+1)sinB=0；③a=2.试从中再选择两个条件以确定ABC，并求出所确定的ABC的面积.

Answer 1

【答案】⑴ ；⑵选择①，③ S△ABC=+1 ；选择②，③ S△ABC=+1； 选择①，②不能确定三角形

【解析】

（1）由⊥，可得，得cosA＝，即可得出；

（2）选择①，③或选择②，③．利用正弦定理与余弦定理、三角形的面积计算公式即可得出．选择①，②不能确定三角形．

（1）∵⊥，∴＝2sinBsinC﹣2cosBcosC﹣＝0，∴cos（B+C）＝﹣，

∴cosA＝，又0°＜A＜180°，∴A＝30°．

（2）选择①，③．∵A═30°，B＝45°，C＝105°，a＝2，且sin105°＝sin（45°+60°）＝，

c＝＝

，∴S△ABC＝acsinB＝+1．

选择②，③．∵A＝30°，a＝2，∴2sinC＝（+1）sinB2c＝（+1）b，

由余弦定理：a2＝4＝b2+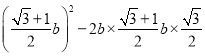 b2＝8 b＝2．

c＝，∴S△ABC＝+1．

选①，②不能确定三角形．