题目内容
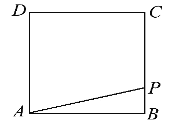
【题目】如图,四边形![]() 是矩形,四边形
是矩形,四边形![]() 是梯形,
是梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() , 点
, 点![]() 是
是![]() 的中点.
的中点.
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析;(2)![]()
【解析】分析:第一问首先应用三角形的中位线的平行性质找到线线平行的关系,之后借助于线面平行的判定定理证得结果;第二问建立适当的空间直角坐标系,借助于平面的法向量所成角的余弦值,求得二面角的余弦值,在最后确定结果时需要判断法向量的方向,是其补角还是其本身.
详解:(1)证明:连结![]() ,交
,交![]() 于点
于点![]() ,∴点
,∴点![]() 是
是![]() 的中点.
的中点.
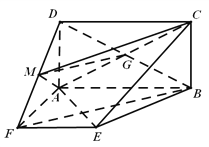
∵点![]() 是
是![]() 的中点,∴
的中点,∴![]() 是△
是△![]() 的中位线. ∴
的中位线. ∴![]()
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]()
(2)![]() 四边形
四边形![]() 是梯形,
是梯形,![]() ,
,![]()
又四边形![]() 是矩形,
是矩形,![]() ,
,
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
∴![]() 平面
平面![]()
以![]() 为原点,以
为原点,以![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]()
轴建立空间直角坐标系,
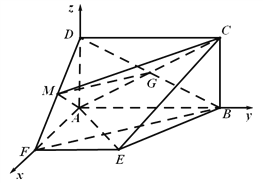
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]()
![]() ,
,
∴![]()
![]() ,
,![]()
![]() .
.
即![]()
令![]() ,则
,则![]() ,
,![]() .∴可取
.∴可取![]()
![]() .
.
又![]() 是平面
是平面![]() 的法向量,
的法向量,
∴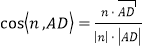
![]() 由图可知,二面角
由图可知,二面角![]() 为锐角.
为锐角.
∴二面角![]() 的余弦值是
的余弦值是![]()

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
【题目】某高校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的60名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | 合计 | |
男生 | 20 | 10 | 30 |
女生 | 10 | 20 | 30 |
合计 | 30 | 30 | 60 |
(1)判断是否有99.5%的把握认为喜欢“应用统计”课程与性别有关?
(2)用分层抽样的方法从喜欢统计课程的学生中抽取6名学生作进一步调查,将这6名学生作为一个样本,从中任选3人,求恰有2个男生和1个女生的概率.
下面的临界值表供参考:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)