题目内容
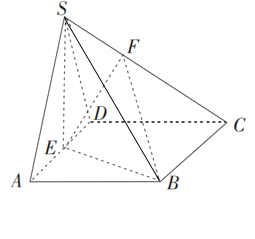
【题目】已知四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,SA=SD=2![]() ,点E是棱AD的中点,点F在棱SC上,且
,点E是棱AD的中点,点F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
(1)求实数λ的值;
(2)求三棱锥F﹣EBC的体积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)连接AC,设AC∩BE=G,根据线面平行的性质定理,结合平行线的性质,通过相似三角形的性质进行求解即可;
(2)根据菱形的性质、勾股定理的逆定理、线面垂直的判定定理,结合三棱锥的体积公式,三角形的面积公式进行求解即可.
(1)连接AC,设AC∩BE=G,则平面SAC∩平面EFB=FG,
∵SA∥平面EFB,∴SA∥FG,
∵△GEA∽△GBC,∴![]() ,
,
∴![]() ,
,
得SF![]() ,即
,即![]() ;
;
(2)∵SA=SD=2![]() ,∴SE⊥AD,SE=4.
,∴SE⊥AD,SE=4.
又∵AB=AD=4,∠BAD=60°,∴BE=2![]() .
.
∴SE2+BE2=SB2,则SE⊥BE.![]() ,
,![]() 平面ABCD,
平面ABCD,
∴SE⊥平面ABCD,
∴![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

