题目内容
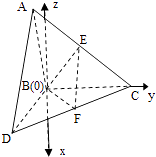
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点. 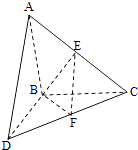
(1)求证:EF⊥BC;
(2)求二面角E﹣BF﹣C的正弦值.
【答案】
(1)证明:由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,易得B(0,0,0),A(0,﹣1, ![]() ),D(
),D( ![]() ,﹣1,0),C(0,2,0),因而E(0,
,﹣1,0),C(0,2,0),因而E(0, ![]() ,
, ![]() ),F(
),F( ![]() ,
, ![]() ,0),所以
,0),所以 ![]() =(
=( ![]() ,0,﹣
,0,﹣ ![]() ),
), ![]() =(0,2,0),因此
=(0,2,0),因此 ![]()
![]() =0,所以EF⊥BC.
=0,所以EF⊥BC.
(2)解:在图中,设平面BFC的一个法向量 ![]() =(0,0,1),平面BEF的法向量
=(0,0,1),平面BEF的法向量 ![]() =(x,y,z),又
=(x,y,z),又 ![]() =(
=( ![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,
, ![]() ),
),
由 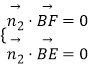 得其中一个
得其中一个 ![]() =(1,﹣
=(1,﹣ ![]() ,1),
,1),
设二面角E﹣BF﹣C的大小为θ,由题意知θ为锐角,则
cosθ=|cos< ![]() ,
, ![]() >|=|
>|=| 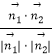 |= ,
|= ,
因此sinθ= ![]() =
= ![]() ,即所求二面角正弦值为
,即所求二面角正弦值为 ![]() .
.
【解析】(1)以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,得到E、F、B、C点的坐标,易求得此 ![]()
![]() =0,所以EF⊥BC;(2)设平面BFC的一个法向量
=0,所以EF⊥BC;(2)设平面BFC的一个法向量 ![]() =(0,0,1),平面BEF的法向量
=(0,0,1),平面BEF的法向量 ![]() =(x,y,z),依题意,可求得一个
=(x,y,z),依题意,可求得一个 ![]() =(1,﹣
=(1,﹣ ![]() ,1),设二面角E﹣BF﹣C的大小为θ,可求得sinθ的值.
,1),设二面角E﹣BF﹣C的大小为θ,可求得sinθ的值.
【考点精析】根据题目的已知条件,利用直线与平面垂直的性质的相关知识可以得到问题的答案,需要掌握垂直于同一个平面的两条直线平行.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.