题目内容
【题目】设Sn是数列{an}的前n项和,且2an+Sn=An2+Bn+C.
(1)当A=B=0,C=1时,求an;
(2)若数列{an}为等差数列,且A=1,C=﹣2. ①设bn=2nan , 求数列{bn}的前n项和;
②设cn= ![]() ,若不等式cn≥
,若不等式cn≥ ![]() 对任意n∈N*恒成立,求实数m的取值范围.
对任意n∈N*恒成立,求实数m的取值范围.
【答案】
(1)解:当A=B=0,C=1时,2an+Sn=1,
∴ ![]() ;
;
当n≥2时,2an﹣1+Sn﹣1=1,
两式作差得:3an=2an﹣1,即 ![]() ,
,
∴数列{an}是以 ![]() 为首项,以
为首项,以 ![]() 为公比的等比数列,
为公比的等比数列,
∴ ![]()
(2)解:当A=1,C=﹣2时,2an+Sn=n2+Bn﹣2,
∴ ![]() ,
, ![]() ,
, ![]() ,
,
∵数列{an}为等差数列,
∴ ![]() ,解得:B=4.
,解得:B=4.
∴a1=1,a2=5,则d=4,
∴an=1+4(n﹣1)=4n﹣3,
① bn=2nan=(4n﹣3)2n,
∴数列{bn}的前n项和 ![]() ,
,
![]() ,
,
两式作差得: ![]()
= ![]() =2﹣16+2n+3﹣(4n﹣3)2n+1,
=2﹣16+2n+3﹣(4n﹣3)2n+1,
∴ ![]() ;
;
②cn= ![]() =
= ![]() =
= ![]() ,
,
∵ ![]() 单调递增,
单调递增,
∴当n=1时, ![]() 有最小值为
有最小值为 ![]() ,
,
∴ ![]() ,即m≤﹣14.
,即m≤﹣14.
∴实数m的取值范围是(﹣∞,﹣14]
【解析】(1)把A=B=0,C=1代入2an+Sn=An2+Bn+C,求得数列首项,进一步可得数列{an}是以 ![]() 为首项,以
为首项,以 ![]() 为公比的等比数列,则数列的通项公式可求;(2)①由已知求出B,得到数列{an}的通项公式,代入bn=2nan , 利用错位相减法求得数列{bn}的前n项和Tn;②把Tn代入cn=
为公比的等比数列,则数列的通项公式可求;(2)①由已知求出B,得到数列{an}的通项公式,代入bn=2nan , 利用错位相减法求得数列{bn}的前n项和Tn;②把Tn代入cn= ![]() ,由函数的单调性求其最小值,由
,由函数的单调性求其最小值,由 ![]() 小于等于cn的最小值求得m的取值范围.
小于等于cn的最小值求得m的取值范围.
【考点精析】通过灵活运用等差数列的通项公式(及其变式)和数列的前n项和,掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系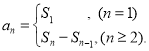 即可以解答此题.
即可以解答此题.

 小学课时特训系列答案
小学课时特训系列答案【题目】一鲜花店根据一个月(30天)某种鲜花的日销售量与销售天数统计如下,将日销售量落入各组区间频率视为概率.
日销售量(枝) |
|
|
|
|
|
销售天数 | 3天 | 5天 | 13天 | 6天 | 3天 |
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的时候选择2天作促销活动,求这2天恰好是在日销售量低于50枝时的概率.