题目内容

【题目】已知函数.

（1）判断的单调性，并说明理由；

（2）判断的奇偶性，并用定义证明；

（3）若不等式对任意恒成立，求实数的取值范围.

【答案】（1）增函数，理由见解析 （2）奇函数，证明见解析 （3）

【解析】

（1）利用函数单调性的定义即可得证.

（2）首先判断定义域关于原点对称，利用函数奇偶性定义即可得证.

（3）由(1)(2)以及分离参数法将不等式转化为对任意恒成立，令，求的最大值即可.

解：（1）是定义域上的增函数.

设任意的，且，则

，

因为,所以，又，所以

即，所以是定义域上的增函数.

（2）是奇函数.

证明：因为，定义域关于原点对称

所以对任意，都有

所以是奇函数.

（3）由（2）知为上的奇函数，所以不等式对任意恒成立，等价于对任意恒成立.

又由（1）知，在定义域上单调递增，

得对任意恒成立即对任意恒成立.

设,

则，故在上的最大值为，

所以实数的取值范围为.

练习册系列答案
相关题目

【题目】 (1)已知正数a，b满足a＋b＝1，求证：a2＋b2≥；

(2)设a、b、c为△ABC的三条边，求证：a2＋b2＋c2<2(ab＋bc＋ca)．

【题目】某高中学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在[50,100]内，发布成绩使用等级制．各等级划分标准见图表．规定：A，B，C三级为合格等级，D为不合格等级.

分数

85分及以上

70分到84分

60分到69分

60分以下

等级

A

B

C

D

为了解该校高一年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计．按照[50,60)，[60,70)，[70,80)，[80,90)，[90,100]的分组作出频率分布直方图如图①所示，样本中原始成绩在80分及以上的所有数据的茎叶图如图②所示．

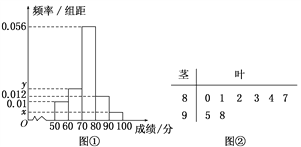
(1)求n和频率分布直方图中的x，y的值，并估计该校高一年级学生成绩是合格等级的概率；

(2)在选取的样本中，从成绩为A，D两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生的成绩是A等级的概率．

【题目】某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元．该公司第年需要付出设备的维修和工人工资等费用的信息如下图．

（1）求；

（2）引进这种设备后，从第几年开始该公司能够获利？

（3）这种设备使用多少年，该公司的年平均获利最大？

【题目】设函数，其中，，为常数．

（1）若，，试讨论函数的单调区间；

（2）若函数在上单调递增，且，证明：，并求的最小值（用，的代数式表示）．

【题目】某工厂生产某种产品的年固定成本为200万元，每生产千件，需另投入成本为，当年产量不足80千件时，（万元）．当年产量不小于80千件时，（万元）．每件商品售价为0.05万元．通过市场分析，该厂生产的商品能全部售完．

（1）写出年利润（万元）关于年产量（千件）的函数解析式；

（2）当年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

【题目】对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到另一点的距离是在南北方向上行进的距离加上在东西方向上行进的距离，这种距离即“曼哈顿距离”，也叫“出租车距离”.对于平面直角坐标系中的点和，两点间的“曼哈顿距离”.

（1）如图，若为坐标原点，，两点坐标分别为和，求，，；

（2）若点满足，试在图中画出点的轨迹，并求该轨迹所围成图形的面积；

（3）已知函数，试在图象上找一点，使得最小，并求出此时点的坐标.

【题目】已知函数，函数.

（1）若函数，最小值为，求实数的值；

（2）当时，不等式的解集为，求实数的取值范围.

【题目】在四棱锥中，,，，为的中点，为的中点，．

（1）求证： 平面；

（2）取中点,证明：平面；

（3）求点到平面的距离.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网