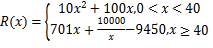题目内容
【题目】对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到另一点的距离是在南北方向上行进的距离加上在东西方向上行进的距离，这种距离即“曼哈顿距离”，也叫“出租车距离”.对于平面直角坐标系中的点
和
，两点间的“曼哈顿距离”
.
（1）如图，若
为坐标原点，
，
两点坐标分别为
和
，求
，
，
；
（2）若点
满足
，试在图中画出点的轨迹，并求该轨迹所围成图形的面积；
（3）已知函数
，试在
图象上找一点
，使得
最小，并求出此时点的坐标.
【答案】（1）5,5,4 （2）图见解析，面积为50； （3）
【解析】
（1）由题中新定义
即可求解
（2）设
点坐标为
，由新定义可得
，即点的轨迹为正方形，从而可求得面积.
（3）由新定义
，利用函数的单调性即可求出最小值，进而求出点的坐标.
解：（1）由题得
，
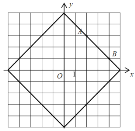
（2）
设点坐标为，因为点满足
，
则，点的轨迹为如图所示正方形（说明：画出图形即可，不用说明理由）
该正方形所围成图形的面积
.
（3）设点坐标为
，则由题
，因为
，
设
，任取
，且
，
则
，
，且，
，
，
在
上是减函数，
当
，即点的坐标为时，
，即
最小为4.
【题目】交强险是车主必须为机动车购买的险种，若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元，在下一年续保时，实行的是费率浮动机制，且保费与上一年度车辆发生道路交通事故的情况相联系．发生交通事故的次数越多，费率也就越高，具体浮动情况如下表：
交强险浮动因素和费率浮动比率表 | ||
浮动因素 | 浮动比率 | |
A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况，随机抽取了60辆车龄已满三年该品牌同型号私家车的下一年续保时的情况，统计得到了下面的表格：
类型 | A1 | A2 | A3 | A4 | A5 | A6 |
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率；
(2)某二手车销售商专门销售这一品牌的二手车，且将下一年的交强险保费高于基本保费的车辆记为事故车．假设购进一辆事故车亏损5 000元，一辆非事故车盈利10 000元．且各种投保类型的频率与上述机构调查的频率一致，完成下列问题：
①若该销售商店内有6辆(车龄已满三年)该品牌二手车，某顾客欲在店内随机挑选2辆车，求这2辆车恰好有一辆为事故车的概率；
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车，求一辆车盈利的平均值．
【题目】某快餐代卖店代售多种类型的快餐，深受广大消费者喜爱.其中，
种类型的快餐每份进价为
元，并以每份
元的价格销售.如果当天20:00之前卖不完，剩余的该种快餐每份以
元的价格作特价处理，且全部售完.
（1）若该代卖店每天定制
份种类型快餐，求种类型快餐当天的利润
（单位：元）关于当天需求量
（单位：份，
）的函数解析式；
（2）该代卖店记录了一个月
天的种类型快餐日需求量（每天20:00之前销售数量）
日需求量 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
（i）假设代卖店在这一个月内每天定制份种类型快餐，求这一个月种类型快餐的日利润（单位：元）的平均数（精确到
）；
（ii）若代卖店每天定制份种类型快餐，以天记录的日需求量的频率作为日需求量发生的概率，求种类型快餐当天的利润不少于
元的概率.
