题目内容
【题目】(![]() 分)如图,在三棱锥
分)如图,在三棱锥![]() 中,底面
中,底面![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:![]() .
.
(Ⅱ)判断在线段![]() 上是否存在点
上是否存在点![]() (与点
(与点![]() 不重合),使得
不重合),使得![]() 为直角三角形?若存在,试找出一个点
为直角三角形?若存在,试找出一个点![]() ,并求
,并求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

【答案】(1)详见解析(2)当![]() 时,
时,![]() 为直角三角形.
为直角三角形.
【解析】
试题分析:(1)根据正三角形的性质可得![]() ,根据勾股定理可得
,根据勾股定理可得![]() ,由线面垂直证的判定定理可得
,由线面垂直证的判定定理可得![]() 平面
平面![]() ,由线面垂直的性质可得结论;(2)在(1)基础上可知平面
,由线面垂直的性质可得结论;(2)在(1)基础上可知平面![]() 与
与![]() 平面的垂直性,所以只需过
平面的垂直性,所以只需过![]() 作交线
作交线![]() 的垂线,由线线垂直
的垂线,由线线垂直![]() 线面垂直,再由线面垂直
线面垂直,再由线面垂直![]() 线线垂直,证明直角三角形的存在性,在上述条件下分别求出
线线垂直,证明直角三角形的存在性,在上述条件下分别求出![]() ,
,![]() ,从而求出
,从而求出![]() 的值即可.
的值即可.
试题解析:
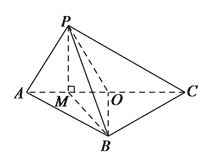
(Ⅰ)证明:如图,连结![]() ,
,
∵在等边![]() 中,
中,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
∴![]() ,
,![]() ,
,
∵在直角![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,且
的中点,且![]() ,
,
∴![]() ,
,
在![]() 中,由
中,由![]() ,得
,得![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() .
.
(Ⅱ)解:线段![]() 上存在点
上存在点![]() 使得
使得![]() 为直角三角形,此时
为直角三角形,此时![]() ,
,
如图,过![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
即![]() 为直角三角形,
为直角三角形,
故当点![]() 与点
与点![]() 重合时,
重合时,![]() 为直角三角形,
为直角三角形,
在直角![]() 中,由
中,由![]() ,
,![]() ,
,![]() ,
,
得![]() (即
(即![]() ),
),![]() (即
(即![]() ),
),
当![]() 时,
时,![]() 为直角三角形.
为直角三角形.
【方法点晴】本题主要考查线面垂直性质与判定、线线垂直的证明,属于难题. 证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.本题的解答一直围绕线面垂直与线线垂直的互相转化进行.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.本题的解答一直围绕线面垂直与线线垂直的互相转化进行.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
