ЬтФПФкШн
ЁОЬтФПЁПФГжабЇИљОн2002Љ2014ФъЦкМфбЇЩњЕФаЫШЄАЎКУЃЌЗжБ№ДДНЈСЫЁАЩугАЁБЁЂЁАЦхРрЁБЁЂЁАЙњбЇЁБШ§ИіЩчЭХЃЌОнзЪСЯЭГМЦаТЩњЭЈЙ§ПМКЫдЖАЮНјШыетШ§ИіЩчЭХГЩЙІгыЗёЯрЛЅЖРСЂЃЌ2015ФъФГаТЩњШыбЇЃЌМйЩшЫћЭЈЙ§ПМКЫбЁАЮНјШыИУаЃЕФЁАЩугАЁБЁЂЁАЦхРрЁБЁЂЁАЙњбЇЁБШ§ИіЩчЭХЕФИХТЪвРДЮЮЊmЃЌ ![]() ЃЌnЃЌвбжЊШ§ИіЩчЭХЫћЖМФмНјШыЕФИХТЪЮЊ
ЃЌnЃЌвбжЊШ§ИіЩчЭХЫћЖМФмНјШыЕФИХТЪЮЊ ![]() ЃЌжСЩйНјШывЛИіЩчЭХЕФИХТЪЮЊ
ЃЌжСЩйНјШывЛИіЩчЭХЕФИХТЪЮЊ ![]() ЃЌЧвmЃОnЃЎ
ЃЌЧвmЃОnЃЎ
ЃЈ1ЃЉЧѓmгыnЕФжЕЃЛ
ЃЈ2ЃЉИУаЃИљОнШ§ИіЩчЭХЛюЖЏАВХХЧщПіЃЌЖдНјШыЁАЩугАЁБЩчЕФЭЌбЇдіМгаЃБОбЁаозжЗж1ЗжЃЌЖдНјШыЁАЦхРрЁБЩчЕФЭЌбЇдіМгаЃБОбЁаобЇЗж2ЗжЃЌЖдНјШыЁАЙњбЇЁБЩчЕФЭЌбЇдіМгаЃБОбЁаобЇЗж3ЗжЃЎЧѓИУаТЭЌбЇдкЩчЭХЗНУцЛёЕУаЃБОбЁаоПЮзжЗжЗжЪ§ЕФЗжВМСаМАЦкЭћЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКгЩЬтвтЃЌ 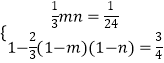 ЃЌmЃОn
ЃЌmЃОn
Ёрm= ![]() ЃЌn=
ЃЌn= ![]()
ЃЈ2ЃЉНтЃКбЇЗжXЕФШЁжЕЗжБ№ЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6ЃЌдђ
PЃЈX=0ЃЉ= ![]() ЃЌPЃЈX=1ЃЉ=
ЃЌPЃЈX=1ЃЉ= ![]() ЁС
ЁС ![]() =
= ![]() ЃЌPЃЈX=2ЃЉ=
ЃЌPЃЈX=2ЃЉ= ![]() ЁС
ЁС ![]() =
= ![]() ЃЌPЃЈX=3ЃЉ=
ЃЌPЃЈX=3ЃЉ= ![]() +
+ ![]() ЁС
ЁС ![]() =
= ![]() ЃЌ
ЃЌ
PЃЈX=4ЃЉ= ![]() ЁС
ЁС ![]() =
= ![]() ЃЌPЃЈX=5ЃЉ=
ЃЌPЃЈX=5ЃЉ= ![]() =
= ![]() ЃЌPЃЈX=6ЃЉ=
ЃЌPЃЈX=6ЃЉ= ![]() ЃЎ
ЃЎ
XЕФЗжВМСа
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P |
|
|
|
|
|
|
|
ЦкЭћEX=0ЁС ![]() +1ЁС
+1ЁС ![]() +2ЁС
+2ЁС ![]() +3ЁС
+3ЁС ![]() +4ЁС
+4ЁС ![]() +5ЁС
+5ЁС ![]() +6ЁС
+6ЁС ![]() =
= ![]()
ЁОНтЮіЁПЃЈ1ЃЉИљОнМйЩшЫћЭЈЙ§ПМКЫбЁАЮНјШыИУаЃЕФЁАЩугАЁБЁЂЁАЦхРрЁБЁЂЁАЙњбЇЁБШ§ИіЩчЭХЕФИХТЪвРДЮЮЊmЃЌ ![]() ЃЌnЃЌвбжЊШ§ИіЩчЭХЫћЖМФмНјШыЕФИХТЪЮЊ
ЃЌnЃЌвбжЊШ§ИіЩчЭХЫћЖМФмНјШыЕФИХТЪЮЊ ![]() ЃЌжСЩйНјШывЛИіЩчЭХЕФИХТЪЮЊ
ЃЌжСЩйНјШывЛИіЩчЭХЕФИХТЪЮЊ ![]() ЃЌЧвmЃОnЃЌНЈСЂЗНГЬзщЃЌМДПЩЧѓmгыnЕФжЕЃЛЃЈ2ЃЉШЗЖЈбЇЗжXЕФПЩФмШЁжЕЃЌЧѓГіЯргІЕФИХТЪЃЌПЩЕУXЕФЗжВМСагыЪ§бЇЦкЭћ
ЃЌЧвmЃОnЃЌНЈСЂЗНГЬзщЃЌМДПЩЧѓmгыnЕФжЕЃЛЃЈ2ЃЉШЗЖЈбЇЗжXЕФПЩФмШЁжЕЃЌЧѓГіЯргІЕФИХТЪЃЌПЩЕУXЕФЗжВМСагыЪ§бЇЦкЭћ

 гХауЩњгІгУЬтПЈПкЫуЬьЬьСЗЯЕСаД№АИ
гХауЩњгІгУЬтПЈПкЫуЬьЬьСЗЯЕСаД№АИ еуНжЎаЧПЮЪБгХЛЏзївЕЯЕСаД№АИ
еуНжЎаЧПЮЪБгХЛЏзївЕЯЕСаД№АИЁОЬтФПЁПФГЙЋНЛЙЋЫОЗжБ№ЭЦГіжЇИЖБІКЭЮЂаХЩЈТыжЇИЖГЫГЕЛюЖЏЃЌЛюЖЏЩшжУСЫвЛЖЮЪБМфЕФЭЦЙуЦкЃЌгЩгкЭЦЙуЦкФкгХЛнСІЖШНЯДѓЃЌЮќв§дНРДдНЖрЕФШЫПЊЪМЪЙгУЩЈТыжЇИЖЃЎФГЯпТЗЙЋНЛГЕЖгЭГМЦСЫЛюЖЏИеЭЦГівЛжмФкУПвЛЬьЪЙгУЩЈТыжЇИЖЕФШЫДЮЃЌгУxБэЪОЛюЖЏЭЦГіЕФЬьЪ§ЃЌyБэЪОУПЬьЪЙгУЩЈТыжЇИЖЕФШЫДЮЃЈЕЅЮЛЃКЪЎШЫДЮЃЉЃЌЭГМЦЪ§ОнШчБэЫљЪОЃК
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y | 6 | 11 | 21 | 34 | 66 | 101 | 196 |
ИљОнвдЩЯЪ§ОнЃЌЛцжЦСЫЩЂЕуЭМЃЎ

ЃЈ1ЃЉИљОнЩЂЕуЭМХаЖЯЃЌдкЭЦЙуЦкФкЃЌ![]() гы
гы![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ОљЮЊДѓгкСуЕФГЃЪ§ЃЉФФвЛИіЪЪвЫзїЮЊЩЈТыжЇИЖЕФШЫДЮ
ОљЮЊДѓгкСуЕФГЃЪ§ЃЉФФвЛИіЪЪвЫзїЮЊЩЈТыжЇИЖЕФШЫДЮ![]() ЙигкЛюЖЏЭЦГіЬьЪ§
ЙигкЛюЖЏЭЦГіЬьЪ§![]() ЕФЛиЙщЗНГЬРраЭЃПЃЈИјГіХаЖЯМДПЩЃЌВЛБиЫЕУїРэгЩЃЉЃЛ
ЕФЛиЙщЗНГЬРраЭЃПЃЈИјГіХаЖЯМДПЩЃЌВЛБиЫЕУїРэгЩЃЉЃЛ
ЃЈ2ЃЉШєyЙигкxЕФЛиЙщЗНГЬВЛЪЧЯпадЕФПЩЭЈЙ§ЛЛдЊЗНЗЈАбЫќЛЏЙщЮЊЯпадЛиЙщЗНГЬЁЃР§ШчЃК![]() ЃЈaЁЂbЮЊГЃЪ§ЃЌeЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЌПЩвдСНБпЭЌЪБШЁздШЛЖдЪ§
ЃЈaЁЂbЮЊГЃЪ§ЃЌeЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЌПЩвдСНБпЭЌЪБШЁздШЛЖдЪ§![]() ЃЌдйСю
ЃЌдйСю![]() ЃЌЯШгУзюаЁЖўГЫЗЈЧѓГі
ЃЌЯШгУзюаЁЖўГЫЗЈЧѓГі![]() гыxЕФЯпадЛиЙщЗНГЬЃЌдйЕУГіyгыxЕФЛиЙщЗНГЬЁЃИљОнЃЈ1ЃЉЕФХаЖЯНсЙћМАБэ1жаЕФЪ§ОнЃЌЧѓyЙигкxЕФЛиЙщЗНГЬЃЛ
гыxЕФЯпадЛиЙщЗНГЬЃЌдйЕУГіyгыxЕФЛиЙщЗНГЬЁЃИљОнЃЈ1ЃЉЕФХаЖЯНсЙћМАБэ1жаЕФЪ§ОнЃЌЧѓyЙигкxЕФЛиЙщЗНГЬЃЛ
ЃЈ3ЃЉгЩ(2)жаЕФЙщЗНГЬдЄВтЛюЖЏЭЦГіЕк12ЬьЪЙгУЩЈТыжЇИЖЕФШЫДЮЁЃ
ВЮПМЪ§ОнЃК
|
|
|
|
|
66 | 1.54 | 2711 | 50.12 | 3.47 |
Цфжа![]() ЃЌВЮПМЙЋЪНЃКЖдгквЛзщЪ§Он
ЃЌВЮПМЙЋЪНЃКЖдгквЛзщЪ§Он![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌЦфЛиЙщжБЯп
ЃЌЦфЛиЙщжБЯп![]() ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊЃК
ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊЃК![]()
 ЃЌ
ЃЌ![]() ЁЃ
ЁЃ

