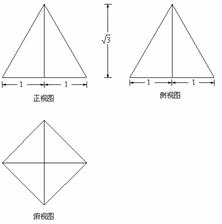
题目内容
已知三棱锥底面是边长为1的正三角形，侧棱长均为2，则侧棱与底面所成角的余弦值为( )
A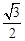． | B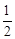． | C． | D． |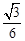
D
分析：由已知易得该三棱锥为正三棱锥，则顶点在底面上的射影正好落在底面的中心上，构造由棱锥高、侧棱长及底面顶点到中心为三边的三角形，解三角形后，即可求出侧棱与底面所成角的余弦值．
解答：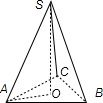
由已知易得该三棱锥为正三棱锥，
则顶点在底面上的射影正好落在底面的中心上
如下图示：
在三棱锥S-ABC中，O为底面中心
则易得SO⊥AO
AO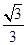
=，SA=2
∠SAO即为侧棱与底面所成的角
则cos∠SAO=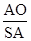
=
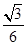
故选D
解答：
由已知易得该三棱锥为正三棱锥，
则顶点在底面上的射影正好落在底面的中心上
如下图示：
在三棱锥S-ABC中，O为底面中心
则易得SO⊥AO
AO
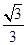=，SA=2∠SAO即为侧棱与底面所成的角
则cos∠SAO=
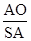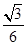
=故选D
练习册系列答案
阅读快车系列答案
相关题目
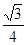a2 D.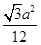 
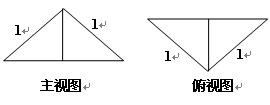
立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，则该几何体的正视图为
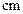）如图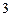
所示，则此几何体的表面积是 
．
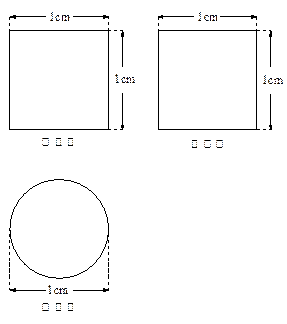
其任意两条母线间夹角的最大值为_________.
)如图所示，
．