题目内容
4.若2a+3b≤2-b+3-a,则a+b≤0(填“<”“>0”或“=”).分析 构造函数f(x)=2x-3-x,根据指数函数的图象和性质得到f(x)在R上为增函数,由f(a)≤f(-b),得到结论.
解答 解:构造函数f(x)=2x-3-x,
因为y=2x为增函数,y=3-x为减函数,
所以f(x)在R上为增函数,
因为2a+3b≤2-b+3-a,
即2a-3-a≤2-b-3b,
∴f(a)≤f(-b),
∴a≤-b,
即a+b≤0,
故答案为:≤
点评 本题考查了指数函数的图象和性质,关键是构造函数,属于中档题.

练习册系列答案
相关题目
16.在△ABC中,a,b,c分别是角A,B,C的对边,a,b,c满足b2=a2+c2-ac,若AC=2$\sqrt{3}$,则△ABC面积的最大值为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
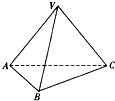 如图,三棱锥V-ABC的底面为正三角形,侧面VAC与底面垂直,且VA=VC,已知其侧(左)视图的面积为$\sqrt{3}$,其正(主)视图的面积为2.
如图,三棱锥V-ABC的底面为正三角形,侧面VAC与底面垂直,且VA=VC,已知其侧(左)视图的面积为$\sqrt{3}$,其正(主)视图的面积为2.