题目内容
14.因式分解:3x2+4xy-y2.分析 首先提取公因式3,再利用配方法把式子变形,然后利用完全平方公式进行分解,再利用平方差公式进行三次分解即可.
解答 解:3x2+4xy-y2
=3(x2+$\frac{4}{3}$xy-$\frac{1}{3}$y2)
=3[(x2+2×$\frac{2}{3}$xy+$\frac{4}{9}$y2)-$\frac{1}{3}$y2-$\frac{4}{9}$y2]
=3[(x+$\frac{2}{3}$y)2-$\frac{7}{9}$y2]
=3(x+$\frac{2}{3}$y+$\frac{\sqrt{7}}{3}$y)(x+$\frac{2}{3}$y-$\frac{\sqrt{7}}{3}$y)
=3[x+$\frac{2+\sqrt{7}}{3}$y)(x-$\frac{2-\sqrt{7}}{3}$y).
点评 此题主要考查了因式分解,关键是掌握分解因式的方法,先提公因式,后用公式法.

练习册系列答案
相关题目
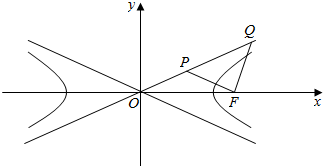
5.如图,已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,P、Q在渐近线上,PQ的中垂线过点F,O是坐标原点,若∠PFQ=Rt∠,OQ=3OP,则双曲线的离心率等于( )

| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
19.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|≤1,且|$\overrightarrow{a}$-$\overrightarrow{b}$|≤$\sqrt{3}$,则$\overrightarrow{a}$•$\overrightarrow{b}$的最小值为( )
| A. | 4-2$\sqrt{3}$ | B. | -2 | C. | 1 | D. | $\frac{1}{2}$ |
15.已知$\overrightarrow{a}$=(1-t,2t-1,0),$\overrightarrow{b}$=(2,t,2t),则|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
16.已知$sinθ=\frac{4}{5}$,$cosθ=-\frac{3}{5}$,则2θ是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |