题目内容
是否存在实数a,使得函数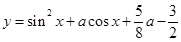 在闭区间
在闭区间 上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由.
上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由.
存在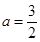 符合题意.
符合题意.
解析试题分析:将原函数化简为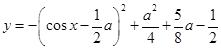 ,令
,令 ,0≤t≤1,可将问题转化为一元二次函数中来解决,
,0≤t≤1,可将问题转化为一元二次函数中来解决, ,其中0≤t≤1,对称轴
,其中0≤t≤1,对称轴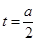 与给定的范围
与给定的范围 进行讨论,得出最值,验证最值是否取到1 即可.
进行讨论,得出最值,验证最值是否取到1 即可.
解: 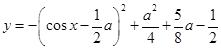 ,
,
当0≤x≤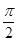 时,0≤cos x≤1,令
时,0≤cos x≤1,令 则0≤t≤1,
则0≤t≤1,
∴ ,0≤t≤1.
,0≤t≤1.
当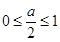 ,即0≤a≤2时,则当
,即0≤a≤2时,则当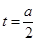 ,即
,即 时.
时.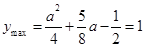 ,解得
,解得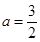 或a=-4(舍去).
或a=-4(舍去).
当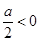 ,即a<0时,则当t=0,即
,即a<0时,则当t=0,即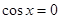 时,
时, ,解得
,解得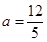 (舍去).
(舍去).
当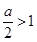 ,即a>2时,则当t=1,即
,即a>2时,则当t=1,即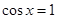 时,
时, ,解得
,解得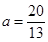 (舍去).
(舍去).
综上知,存在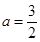 符合题意.
符合题意.
考点:同角三角函数的基本关系式,二次函数求最值.

练习册系列答案
相关题目
某同学用“五点法”画函数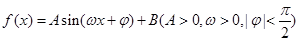 在某一
在某一
个周期内的图象时,列表并填入的部分数据如下表:
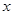 | 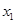 | 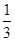 | 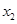 | 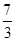 | 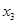 |
 |  | 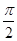 | 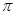 | 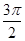 | 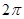 |
 |  | 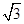 |  | 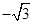 |  |
(1)请求出上表中的
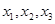 ,并直接写出函数
,并直接写出函数 的解析式;
的解析式;(2)将
 的图象沿
的图象沿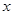 轴向右平移
轴向右平移 个单位得到函数
个单位得到函数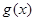 ,若函数
,若函数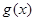 在
在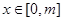 (其中
(其中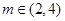 )上的值域为
)上的值域为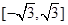 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为 ,求
,求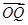 与
与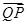 夹角
夹角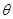 的大小.
的大小.  的一段图象过点(0,1),如图所示.(1)求函数
的一段图象过点(0,1),如图所示.(1)求函数 的表达式;(2)将函数
的表达式;(2)将函数 的图象向右平移
的图象向右平移 个单位,得函数
个单位,得函数 的图象,求
的图象,求
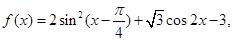
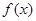 的最小正周期;
的最小正周期;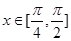 时,求
时,求 +
+ +
+ (
( 为常数)
为常数) 的最小正周期;
的最小正周期; 上的最大值与最小值之和为
上的最大值与最小值之和为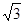 ,求实数
,求实数 的值.
的值. ﹣x)满足
﹣x)满足 ,求函数f(x)在
,求函数f(x)在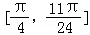 上的最大值和最小值.
上的最大值和最小值. ,
,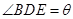 ,
,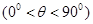 .
.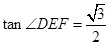 时,求
时,求 的大小;
的大小;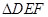 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时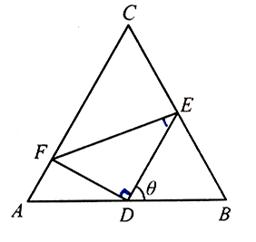
 (其中
(其中 >0,
>0, ),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
),且f(x)的图象在y轴右侧的第一个最高点的横坐标为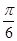 .
.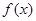 在区间
在区间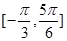 的最小值为
的最小值为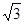 ,求
,求 的值.
的值.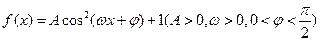 的最大值为3,
的最大值为3, 的图像的相邻两对称轴间的距离为2,在
的图像的相邻两对称轴间的距离为2,在 轴上的截距为2.
轴上的截距为2.