题目内容
设函数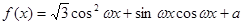 (其中
(其中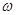 >0,
>0,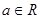 ),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
),且f(x)的图象在y轴右侧的第一个最高点的横坐标为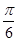 .
.
(1)求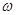 的值;
的值;
(2)如果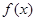 在区间
在区间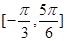 的最小值为
的最小值为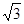 ,求
,求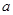 的值.
的值.
(1) =
=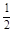 ;(2)a=
;(2)a= .
.
解析试题分析:(1)对函数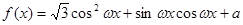 进行化简,得到f(x)==sin(2
进行化简,得到f(x)==sin(2 x+
x+ )+
)+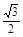 +a,得到2
+a,得到2 ·
·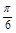 +
+ =
= ,即可求出
,即可求出 的值;(2)由(1)知f(x)=sin(2
的值;(2)由(1)知f(x)=sin(2 x+
x+ )+
)+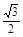 +a,当x∈
+a,当x∈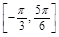 时,x+
时,x+ ∈
∈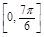 ,故-
,故-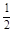 ≤sin(x+
≤sin(x+ )≤1,从而f(x)在
)≤1,从而f(x)在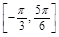 上取得最小值-
上取得最小值-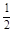 +
+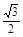 +a,因此,由题设知-
+a,因此,由题设知-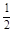 +
+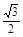 +a=
+a= ,即可求出a的值.
,即可求出a的值.
解:(1) f(x)=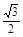 cos2
cos2 x+
x+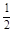 sin2
sin2 x+
x+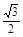 +a .2
+a .2
=sin(2 x+
x+ )+
)+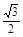 +a ..4
+a ..4
依题意得2 ·
·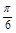 +
+ =
= 解得
解得 =
=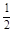 .6
.6
(2) 由(1)知f(x)=sin(2 x+
x+ )+
)+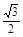 +a
+a
又当x∈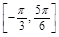 时,x+
时,x+ ∈
∈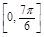 8
8
故-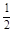 ≤sin(x+
≤sin(x+ )≤1 ..10
)≤1 ..10
从而f(x)在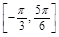 上取得最小值-
上取得最小值-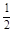 +
+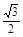 +a
+a
因此,由题设知-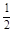 +
+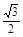 +a=
+a= 故a=
故a= .12
.12
考点:1.三角函数恒等变换;2.三角函数的最值.

练习册系列答案
相关题目
 在闭区间
在闭区间 上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由.
上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由.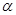 的终边过点
的终边过点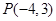 .
.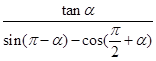 的值;
的值;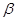 为第三象限角,且
为第三象限角,且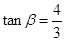 ,求
,求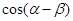 的值.
的值.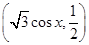 ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.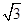 ,c=4,且f(A)是函数f(x)在
,c=4,且f(A)是函数f(x)在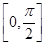 上的最大值,求△ABC的面积S.
上的最大值,求△ABC的面积S.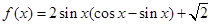 ,
,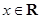 .
.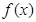 的最小正周期和单调增区间;
的最小正周期和单调增区间;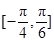 上的最小值和最大值;
上的最小值和最大值;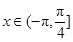 ,求使
,求使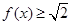 的
的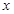 取值范围.
取值范围.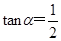 ,求
,求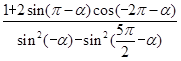 的值.
的值.
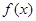 的最小正周期;
的最小正周期;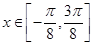 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。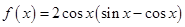 .
.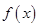 的最小正周期;
的最小正周期; , 设函数
, 设函数 .
.  上的最大值和最小值.
上的最大值和最小值.