题目内容
函数 的一段图象过点(0,1),如图所示.(1)求函数
的一段图象过点(0,1),如图所示.(1)求函数 的表达式;(2)将函数
的表达式;(2)将函数 的图象向右平移
的图象向右平移 个单位,得函数
个单位,得函数 的图象,求
的图象,求 的最大值,并求出此时自变量x的集合.
的最大值,并求出此时自变量x的集合.
(1)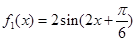 ;(2)
;(2) .
.
解析试题分析:(1)根据题中的信息可知,周期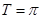 ,于是
,于是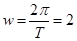 ,又当
,又当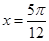 为函数的一个零点,根据正弦函数图像的性质,可得
为函数的一个零点,根据正弦函数图像的性质,可得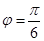 ,最后根据图像过(0,1)可得
,最后根据图像过(0,1)可得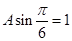 ,即A=2,从而
,即A=2,从而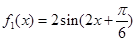 .;(2)由函数图像平移的规律可得
.;(2)由函数图像平移的规律可得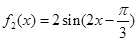 ,再根据正弦函数
,再根据正弦函数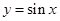 的性质,当
的性质,当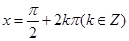 时,y取到最大值,因此,对于
时,y取到最大值,因此,对于 ,当
,当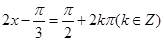 时取到最大值,从而可以求得所求集合为
时取到最大值,从而可以求得所求集合为 .
.
(1)由题图知,周期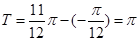 ,于是
,于是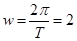 ,又当
,又当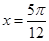 时,
时,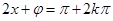 ,∴
,∴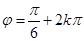 ,又∵
,又∵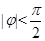 ,∴
,∴ ,又∵图像过(0,1),∴
,又∵图像过(0,1),∴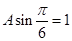 ,A=2,∴
,A=2,∴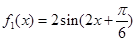 ;
;
(2)依题意,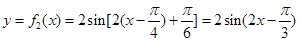 .
.
∴当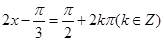 时,y有最大值2,解得:
时,y有最大值2,解得: ,
,
∴x取值集合为 .
.
考点:1、三角函数的图像与性质;2、函数图像平移规律.

练习册系列答案
相关题目
 ;求
;求 的值.
的值. ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.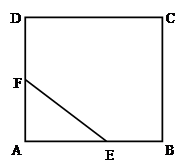

 ,
, .
. 的值;
的值; 的最大值和最小正周期;
的最大值和最小正周期; ,
, 是第二象限的角,求
是第二象限的角,求 .
.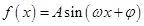 ,x∈R(其中A>0,ω>0,
,x∈R(其中A>0,ω>0,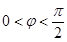 )的周期为π,且图象上一个最低点为M
)的周期为π,且图象上一个最低点为M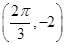 .
. 时,求f(x)的最大值.
时,求f(x)的最大值.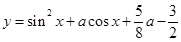 在闭区间
在闭区间 上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由.
上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由.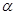 的终边过点
的终边过点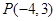 .
.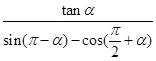 的值;
的值;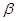 为第三象限角,且
为第三象限角,且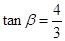 ,求
,求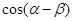 的值.
的值.