题目内容
某同学用“五点法”画函数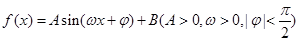 在某一
在某一
个周期内的图象时,列表并填入的部分数据如下表:
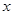 | 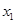 | 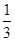 | 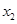 | 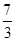 | 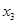 |
 |  | 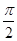 | 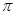 | 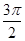 | 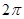 |
 |  | 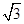 |  | 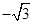 |  |
(1)请求出上表中的
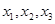 ,并直接写出函数
,并直接写出函数 的解析式;
的解析式;(2)将
 的图象沿
的图象沿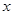 轴向右平移
轴向右平移 个单位得到函数
个单位得到函数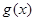 ,若函数
,若函数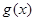 在
在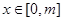 (其中
(其中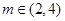 )上的值域为
)上的值域为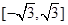 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为 ,求
,求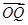 与
与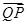 夹角
夹角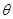 的大小.
的大小.
(1)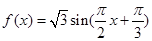 ;(2)
;(2) .
.
解析试题分析:本题主要考查五点作图法、三角函数图象的平移、三角函数值域、向量的夹角公式等基础知识,考查学生的分析问题解决问题的能力、计算能力,考查学生的数形结合思想.第一问,结合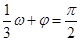 且
且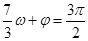 ,得出
,得出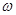 和
和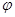 ,再解方程求出
,再解方程求出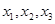 的值,再结合三角函数图象写出
的值,再结合三角函数图象写出 解析式;第二问,先将
解析式;第二问,先将 图象向右平移得到
图象向右平移得到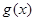 解析式,结合正弦图象,利用值域确定最高点、最低点的坐标,从而得到
解析式,结合正弦图象,利用值域确定最高点、最低点的坐标,从而得到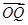 和
和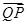 向量坐标,利用夹角公式求出
向量坐标,利用夹角公式求出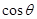 ,再确定角
,再确定角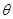 .
.
试题解析:(1)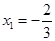 ,
, ,
,

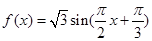
(2)将 的图像沿
的图像沿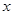 轴向右平移
轴向右平移 个单位得到函数
个单位得到函数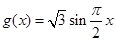
由于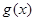 在
在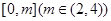 上的值域为
上的值域为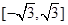 ,
,
则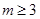 ,故最高点为
,故最高点为 ,最低点为
,最低点为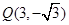 .
.
则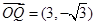 ,
,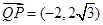 ,则
,则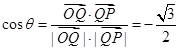
故 .
.
考点:五点作图法、三角函数图象的平移、三角函数值域、向量的夹角公式.

练习册系列答案
相关题目

 ,
,
 ;求
;求 的值.
的值. .
. 的最小正周期;
的最小正周期; 时,求
时,求
 的值域;
的值域; 的最大值和最小值.
的最大值和最小值. ,
, ,且
,且 .
. 的值;
的值; ,
, ,求
,求 .
. ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.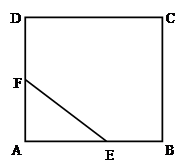

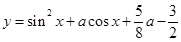 在闭区间
在闭区间 上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由.
上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由.