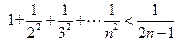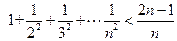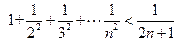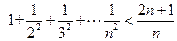题目内容
(本小题满分14分)
已知函数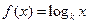 (
(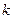 为常数,
为常数,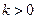 且
且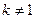 ),且数列
),且数列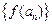 是首项为4,
是首项为4,
公差为2的等差数列.
(Ⅰ)求证:数列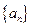 是等比数列;
是等比数列;
(Ⅱ)若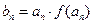 ,当
,当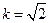 时,求数列
时,求数列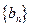 的前
的前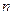 项和
项和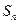 ;
;
(III)若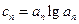 ,且
,且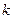 >1,比较
>1,比较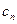 与
与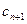 的大小.
的大小.
已知函数
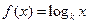 (
(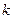 为常数,
为常数,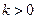 且
且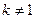 ),且数列
),且数列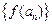 是首项为4,
是首项为4,公差为2的等差数列.
(Ⅰ)求证:数列
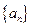 是等比数列;
是等比数列;(Ⅱ)若
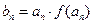 ,当
,当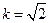 时,求数列
时,求数列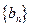 的前
的前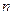 项和
项和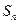 ;
;(III)若
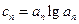 ,且
,且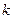 >1,比较
>1,比较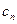 与
与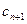 的大小.
的大小.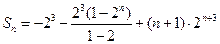
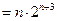 ,
,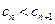
(Ⅰ)证:由题意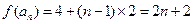 ,即
,即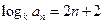 , ……2分
, ……2分
∴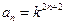 ∴
∴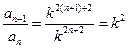 . ……4分
. ……4分
∵常数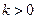 且
且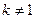 ,∴
,∴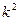 为非零常数,
为非零常数,
∴数列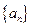 是以
是以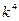 为首项,
为首项,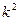 为公比的等比数列. ……6分
为公比的等比数列. ……6分
(II) 解:由(1)知, ,
,
当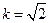 时,
时,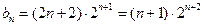 . …………7分
. …………7分
∴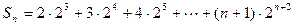 , ①
, ①
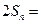
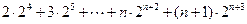 . ② ……9分
. ② ……9分
②-①,得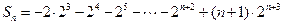
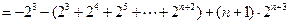
∴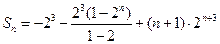
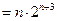 . ……11分
. ……11分
(III)解:由(1)知,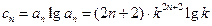 ;当
;当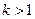 时,
时,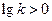 ,
,
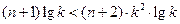 对一切
对一切 成立,即
成立,即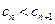 对一切
对一切 成立.…14分
成立.…14分
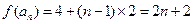 ,即
,即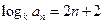 , ……2分
, ……2分∴
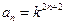 ∴
∴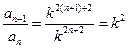 . ……4分
. ……4分∵常数
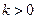 且
且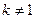 ,∴
,∴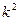 为非零常数,
为非零常数,∴数列
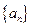 是以
是以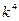 为首项,
为首项,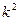 为公比的等比数列. ……6分
为公比的等比数列. ……6分(II) 解:由(1)知,
 ,
,当
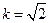 时,
时,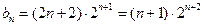 . …………7分
. …………7分∴
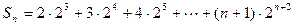 , ①
, ①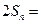
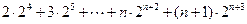 . ② ……9分
. ② ……9分②-①,得
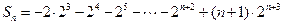
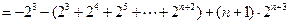
∴
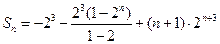
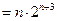 . ……11分
. ……11分(III)解:由(1)知,
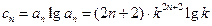 ;当
;当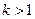 时,
时,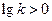 ,
,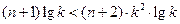 对一切
对一切 成立,即
成立,即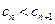 对一切
对一切 成立.…14分
成立.…14分
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
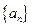 为等差数列,
为等差数列,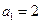 ,且其前10项和为65,又正项数列
,且其前10项和为65,又正项数列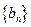 满足
满足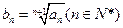 .
.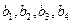 的大小;
的大小;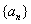 、
、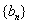 满足:
满足: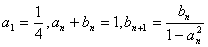 .
.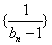 是等差数列;
是等差数列;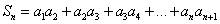 ,若
,若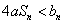 对于
对于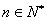 恒成立,试求实数
恒成立,试求实数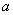 的取值范围
的取值范围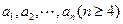 是各项均不为零的等差
是各项均不为零的等差 数列,且公差
数列,且公差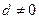 .设
.设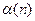 是将此数列删去某一项得到的数列(按原来的顺序)为等比数列的最大的
是将此数列删去某一项得到的数列(按原来的顺序)为等比数列的最大的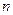 值,则
值,则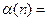
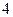 B.
B.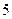
 C.
C.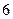 D.
D.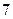
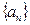 中,有
中,有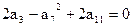 ,数列
,数列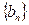 是等比数列,且
是等比数列,且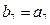 则
则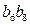 =" ( " )
=" ( " )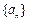 ,
,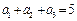 ,
,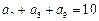 ,则
,则 (※)
(※)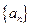 中,
中,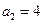 ,对任意正整数
,对任意正整数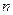 都有
都有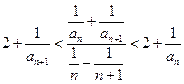 恒成立,则数列
恒成立,则数列 = 。
= 。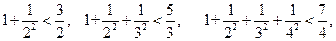 …,
…,