题目内容
(本题满分14分)已知数列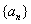 、
、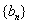 满足:
满足: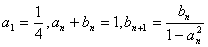 .
.
(1)求证:数列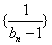 是等差数列;
是等差数列;
(2)求数列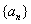 的通项公式;
的通项公式;
(3)设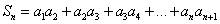 ,若
,若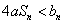 对于
对于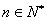 恒成立,试求实数
恒成立,试求实数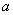 的取值范围
的取值范围
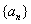 、
、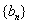 满足:
满足: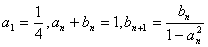 .
.(1)求证:数列
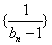 是等差数列;
是等差数列;(2)求数列
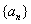 的通项公式;
的通项公式;(3)设
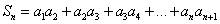 ,若
,若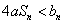 对于
对于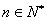 恒成立,试求实数
恒成立,试求实数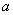 的取值范围
的取值范围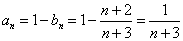
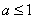 ,
, 对于
对于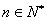 恒成立。
恒成立。解:(1)由
依题意
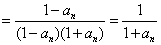
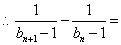
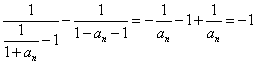
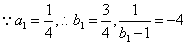 ,
, 数列
数列 是以
是以 为首项公差为
为首项公差为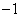 的等差数列
的等差数列
(2)由(1)知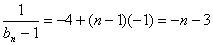
则 ,
,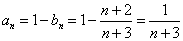
(3)
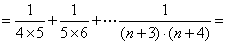
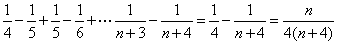

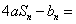
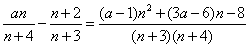
依题意可知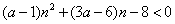 恒成立,令
恒成立,令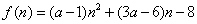
当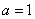 时,
时,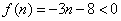 恒成立
恒成立
当 时,由二次函数性质知
时,由二次函数性质知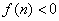 不可能成立
不可能成立
当 时,此二次函数的对称轴为
时,此二次函数的对称轴为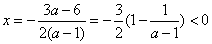
则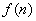 在
在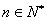 上是单调递减,
上是单调递减, 要使
要使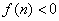 对
对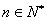 恒成立
恒成立
必须且只须 即
即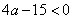 ,
,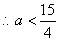 ,又
,又

综上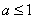 ,
, 对于
对于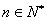 恒成立。
恒成立。

依题意

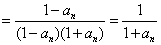
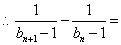
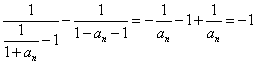
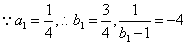 ,
, 数列
数列 是以
是以 为首项公差为
为首项公差为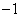 的等差数列
的等差数列(2)由(1)知
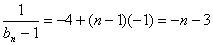
则
 ,
,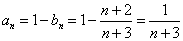
(3)

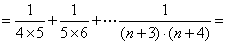
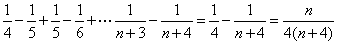

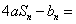
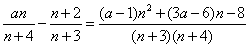
依题意可知
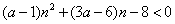 恒成立,令
恒成立,令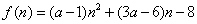
当
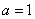 时,
时,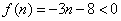 恒成立
恒成立当
 时,由二次函数性质知
时,由二次函数性质知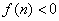 不可能成立
不可能成立当
 时,此二次函数的对称轴为
时,此二次函数的对称轴为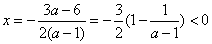
则
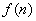 在
在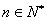 上是单调递减,
上是单调递减, 要使
要使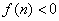 对
对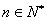 恒成立
恒成立必须且只须
 即
即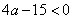 ,
,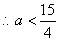 ,又
,又

综上
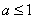 ,
, 对于
对于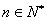 恒成立。
恒成立。
练习册系列答案
相关题目
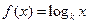 (
(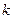 为常数,
为常数,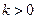 且
且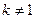 ),且数列
),且数列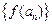 是首项为4,
是首项为4,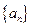 是等比数列;
是等比数列;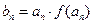 ,当
,当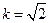 时,求数列
时,求数列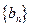 的前
的前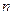 项和
项和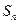 ;
;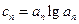 ,且
,且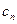 与
与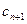 的大小.
的大小.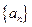 的首项
的首项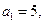 前
前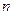 项和为
项和为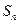 ,且
,且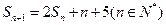
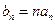 ,求数列
,求数列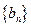 的前n项和
的前n项和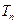 .
. 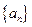 中,
中,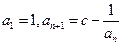 .
.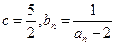 ,求数列
,求数列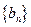 的通项公式;
的通项公式;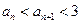 成立的
成立的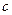 的取值范围.
的取值范围. ,对于任意的
,对于任意的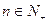 ,都有
,都有 .
.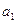 的取值范围;
的取值范围;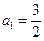 ,证明
,证明 ;
; .
. 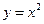 在点
在点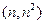 处的切线方程为
处的切线方程为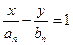 ,其中
,其中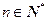
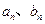 关于
关于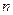 的表达式;
的表达式;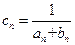 ,求证:
,求证: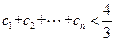 ;
;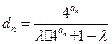 ,其中
,其中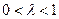 ,求证:
,求证: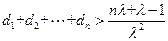

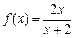 ,
,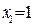 ,
, ,先计算
,先计算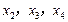 ,后猜想得
,后猜想得 _
_ 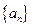 满足
满足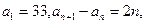 则
则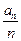 的最小值为__________.
的最小值为__________.