题目内容
(本小题满分14分)已知数列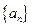 为等差数列,
为等差数列,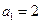 ,且其前10项和为65,又正项数列
,且其前10项和为65,又正项数列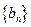 满足
满足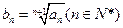 .
.
⑴求数列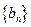 的通项公式;
的通项公式;
⑵比较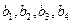 的大小;
的大小;
⑶求数列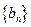 的最大项.
的最大项.
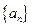 为等差数列,
为等差数列,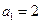 ,且其前10项和为65,又正项数列
,且其前10项和为65,又正项数列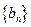 满足
满足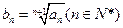 .
.⑴求数列
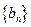 的通项公式;
的通项公式;⑵比较
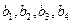 的大小;
的大小;⑶求数列
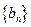 的最大项.
的最大项. ,
,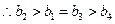 ,
,
解:⑴设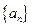 的公差为
的公差为 ,则
,则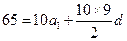 ,又
,又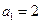 ,得
,得 ,从而
,从而
故 . ……4分
. ……4分
⑵ ,
, ,
,
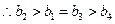 . ……8分
. ……8分
⑶由(2)猜想 递减,即猜想当
递减,即猜想当 时,
时, . ……10分
. ……10分
考察函数 ,则
,则 时,
时, ,
,
故 在
在 上是减函数,而
上是减函数,而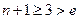 , ……12分
, ……12分
所以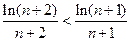 ,即
,即 .
.
猜想正确,因此,数列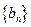 的最大项是
的最大项是 . ……14分
. ……14分
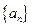 的公差为
的公差为 ,则
,则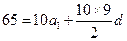 ,又
,又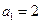 ,得
,得 ,从而
,从而
故
 . ……4分
. ……4分⑵
 ,
, ,
,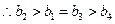 . ……8分
. ……8分⑶由(2)猜想
 递减,即猜想当
递减,即猜想当 时,
时, . ……10分
. ……10分考察函数
 ,则
,则 时,
时, ,
,故
 在
在 上是减函数,而
上是减函数,而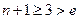 , ……12分
, ……12分所以
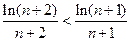 ,即
,即 .
.猜想正确,因此,数列
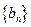 的最大项是
的最大项是 . ……14分
. ……14分
练习册系列答案
相关题目
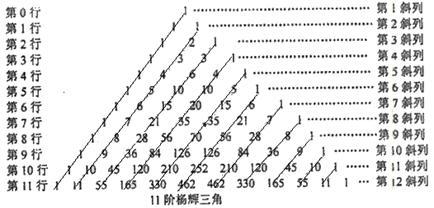
 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为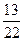 ,求
,求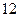 行所有数的和,写出
行所有数的和,写出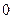 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;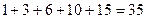 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第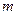 斜列中(从右上到左下)前
斜列中(从右上到左下)前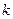 个数之和,一定等于第
个数之和,一定等于第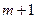 斜列中第
斜列中第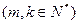 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.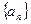 是等和数列,且
是等和数列,且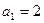 ,公和为
,公和为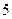 ,求
,求 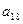 的值,并猜出这个数列的通项公式(不要求证明)。
的值,并猜出这个数列的通项公式(不要求证明)。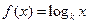 (
(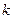 为常数,
为常数,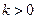 且
且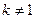 ),且数列
),且数列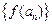 是首项为4,
是首项为4,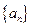 是等比数列;
是等比数列;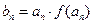 ,当
,当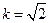 时,求数列
时,求数列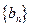 的前
的前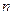 项和
项和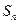 ;
;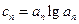 ,且
,且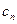 与
与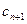 的大小.
的大小.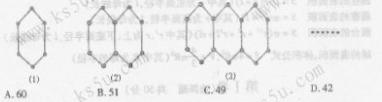
 }中,
}中,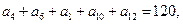 则
则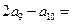
 ,对于任意的
,对于任意的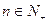 ,都有
,都有 .
.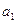 的取值范围;
的取值范围;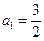 ,证明
,证明 ;
; .
.