题目内容
(本小题满分13分)
如图,设抛物线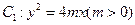 的准线与
的准线与 轴交于
轴交于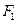 ,焦点为
,焦点为 ;以
;以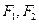 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆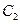 与抛物线
与抛物线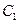 在
在 轴上方的交点为
轴上方的交点为 ,延长
,延长 交抛物线于点
交抛物线于点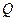 ,
, 是抛物线
是抛物线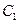 上一动点,且M在
上一动点,且M在 与
与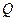 之间运动.
之间运动.
(1)当 时,求椭圆
时,求椭圆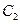 的方程;
的方程;
(2)当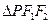 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求 面积的最大值.
面积的最大值.
如图,设抛物线
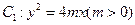 的准线与
的准线与 轴交于
轴交于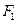 ,焦点为
,焦点为 ;以
;以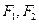 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆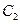 与抛物线
与抛物线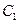 在
在 轴上方的交点为
轴上方的交点为 ,延长
,延长 交抛物线于点
交抛物线于点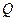 ,
, 是抛物线
是抛物线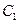 上一动点,且M在
上一动点,且M在 与
与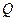 之间运动.
之间运动.(1)当
 时,求椭圆
时,求椭圆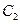 的方程;
的方程;(2)当
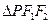 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求 面积的最大值.
面积的最大值.解析:(1)当 时,
时, 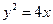 ,则
,则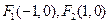 ,
,
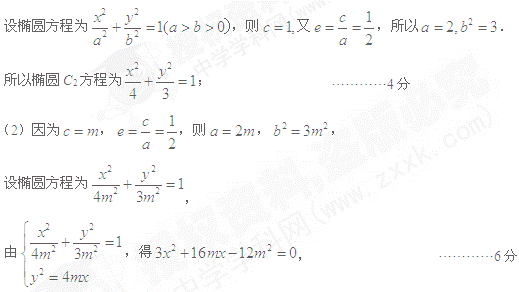 即
即 ,得
,得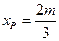 ,代入抛物线方程得
,代入抛物线方程得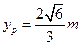 ,即
,即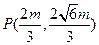 ,
,
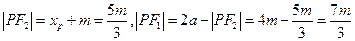 ,
,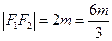 ,
,
因为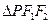 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以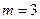 . …………8分
. …………8分

则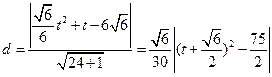 …………11分
…………11分
当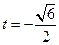 时,
时,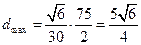 ,
,
即 面积的最大值为
面积的最大值为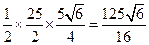 . …………13分
. …………13分
 时,
时, 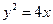 ,则
,则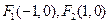 ,
,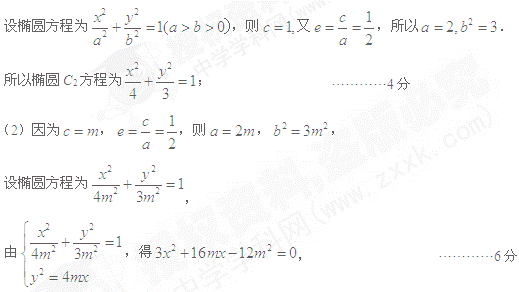 即
即 ,得
,得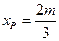 ,代入抛物线方程得
,代入抛物线方程得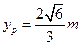 ,即
,即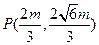 ,
,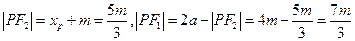 ,
,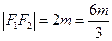 ,
,因为
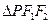 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以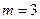 . …………8分
. …………8分
则
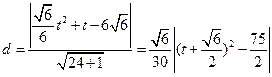 …………11分
…………11分当
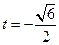 时,
时,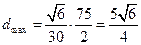 ,
,即
 面积的最大值为
面积的最大值为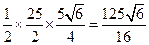 . …………13分
. …………13分略

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 ,动点
,动点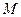 、
、 分别在
分别在 、
、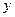 轴上运动,满足
轴上运动,满足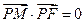 ,
, 为动点,并且满足
为动点,并且满足 .
. 的方程;
的方程;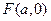 的直线
的直线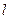 (不与
(不与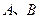 两点,设点
两点,设点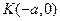 ,
,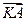 与
与 的夹角为
的夹角为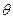 ,求证:
,求证: .
.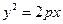 (
(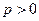 )的焦点为椭圆
)的焦点为椭圆 的右焦点,点
的右焦点,点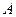 、
、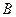 为抛物线上的两点,
为抛物线上的两点,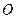 是抛物线的顶点,
是抛物线的顶点,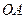 ⊥
⊥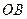 .
.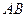 过定点
过定点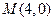 ;
;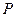 ,求点
,求点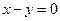 的距离的最小值.
的距离的最小值. -1,m
-1,m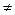 0).
0). , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为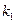 的直线
的直线 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为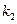 ,求证
,求证 为定值;
为定值;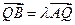 ,且
,且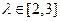 ,求
,求 (p>0)过点C,求焦点F到直线AB的距离.
(p>0)过点C,求焦点F到直线AB的距离. 的焦点为顶点,以椭圆
的焦点为顶点,以椭圆 的顶点为焦点的双曲线方程为
的顶点为焦点的双曲线方程为 的两个顶点为
的两个顶点为 ,
,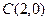 ,周长为12.
,周长为12.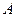 的轨迹
的轨迹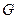 方程;
方程;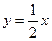 与点
与点 、
、 两点,求
两点,求 的面积.
的面积.