题目内容
【题目】给出下列说法:
(1)命题“![]() ,
,![]() ”的否定形式是“
”的否定形式是“![]() ,
,![]() ”;
”;
(2)已知![]() ,则
,则![]() ;
;
(3)已知回归直线的斜率的估计值是2,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() ;
;
(4)对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大;
有关系”的把握越大;
(5)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变.
其中正确说法的个数为( )
A.2B.3C.4D.5
【答案】B
【解析】
根据含有一个量词的命题的否定,直接判断(1)错;根据正态分布的特征,直接判断(2)对;根据线性回归方程的特点,判断(3)正确;根据独立性检验的基本思想,可判断(4)错;根据方差的特征,可判断(5)正确.
(1)命题“![]() ,
,![]() ”的否定形式是“
”的否定形式是“![]() ,
,![]() ”,故(1)错;
”,故(1)错;
(2)因为![]() ,即
,即![]() 服从正态分布,均值为
服从正态分布,均值为![]() ,所以
,所以![]() ;故(2)正确;
;故(2)正确;
(3)因为回归直线必过样本中心,又已知回归直线的斜率的估计值是2,样本点的中心为![]() ,所以
,所以![]() ,即所求回归直线方程为:
,即所求回归直线方程为:![]() ;故(3)正确;
;故(3)正确;
(4)对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大;故(4)错;
有关系”的把握越大;故(4)错;
(5)若将一组样本数据中的每个数据都加上同一个常数后,方差不变.故(5)错.
故选:B.

【题目】为了调查生活规律与患胃病是否与有关,某同学在当地随机调查了200名30岁以上的人,并根据调查结果制成了不完整的列联表如下:
不患胃病 | 患胃病 | 总计 | |
生活有规律 | 60 | 40 | |
生活无规律 | 60 | 100 | |
总计 | 100 |
(1)补全列联表中的数据;
(2)用独性检验的基本原理,说明生活无规律与患胃病有关时,出错的概率不会超过多少?
参考公式和数表如下:
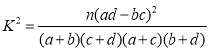
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为研究女高中生身高与体重之间的关系,一调查机构从某中学中随机选取8名女高中生,其身高![]() 和体重
和体重![]() 数据如下表所示:
数据如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 164 | 160 | 158 | 172 | 162 | 164 | 174 | 166 |
体重 | 60 | 46 | 43 | 48 | 48 | 50 | 61 | 52 |
该调查机构绘制出该组数据的散点图后分析发现,女高中生的身高与体重之间有较强的线性相关关系.

(1)调查员甲计算得出该组数据的线性回归方程为![]() ,请你据此预报一名身高为
,请你据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(2)调查员乙仔细观察散点图发现,这8名同学中,编号为1和4的两名同学对应的点与其他同学对应的点偏差太大,于是提出这样的数据应剔除,请你按照这名调查人员的想法重新计算线性回归话中,并据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(3)请你分析一下,甲和乙谁的模型得到的预测值更可靠?说明理由.
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: .
.