题目内容
(本题满分12分)
已知函数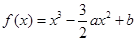 ,
,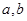 为实数,
为实数,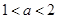 .
.
(Ⅰ)若 在区间
在区间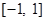 上的最小值、最大值分别为
上的最小值、最大值分别为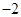 、1,求
、1,求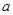 、
、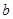 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求经过点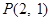 且与曲线
且与曲线 相切的直线
相切的直线 的方程;
的方程;
(Ⅲ)设函数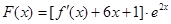 ,试判断函数
,试判断函数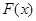 的极值点个数.
的极值点个数.
已知函数
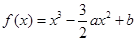 ,
,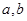 为实数,
为实数,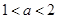 .
.(Ⅰ)若
 在区间
在区间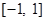 上的最小值、最大值分别为
上的最小值、最大值分别为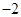 、1,求
、1,求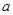 、
、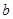 的值;
的值;(Ⅱ)在(Ⅰ)的条件下,求经过点
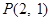 且与曲线
且与曲线 相切的直线
相切的直线 的方程;
的方程;(Ⅲ)设函数
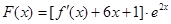 ,试判断函数
,试判断函数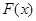 的极值点个数.
的极值点个数.(Ⅰ)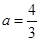 ,
,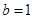 为所求. (Ⅱ)
为所求. (Ⅱ)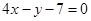 或
或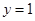 .
.
(Ⅲ)当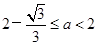 时,
时,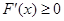 ,函数
,函数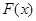 为单调递增,极值点个数为0;
为单调递增,极值点个数为0;
当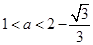 时,此时方程
时,此时方程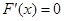 有两个不相等的实数根,根据极值点的定义,
有两个不相等的实数根,根据极值点的定义,
可知函数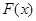 有两个极值点.
有两个极值点.
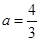 ,
,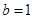 为所求. (Ⅱ)
为所求. (Ⅱ)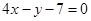 或
或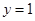 .
. (Ⅲ)当
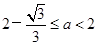 时,
时,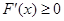 ,函数
,函数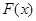 为单调递增,极值点个数为0;
为单调递增,极值点个数为0;当
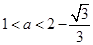 时,此时方程
时,此时方程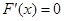 有两个不相等的实数根,根据极值点的定义,
有两个不相等的实数根,根据极值点的定义,可知函数
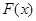 有两个极值点.
有两个极值点.本试题主要考查了导数在研究函数中的运用。
(1)因为函数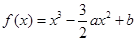 ,
,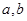 为实数,
为实数,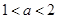 .求解导数。判定单调性和最值,结合
.求解导数。判定单调性和最值,结合 在区间
在区间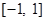 上的最小值、最大值分别为
上的最小值、最大值分别为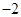 、1得到参数
、1得到参数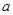 、
、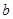 的值;
的值;
(2)在(Ⅰ)的条件下,先求解导数值,然后得到经过点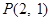 且与曲线
且与曲线 相切的直线
相切的直线 的方程;
的方程;
(Ⅲ)设函数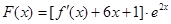 ,函数
,函数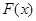 的极值点个数就是分析单调性来得到结论。
的极值点个数就是分析单调性来得到结论。
解:(Ⅰ)由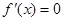 ,得
,得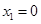 ,
,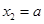 .
.
∵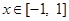 ,
,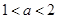 ,
,
∴ 当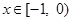 时,
时,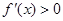 ,
, 递增;
递增;
当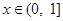 时,
时,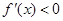 ,
, 递减.
递减.
∴ 在区间
在区间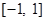 上的最大值为
上的最大值为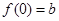 ,∴
,∴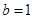 .……………………2分
.……………………2分
又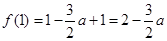 ,
,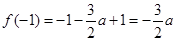 ,∴
,∴ 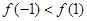 .
.
由题意得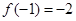 ,即
,即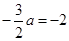 ,得
,得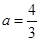 .
.
故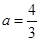 ,
,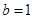 为所求. ………………………………4分
为所求. ………………………………4分
(Ⅱ)解:由(1)得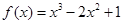 ,
,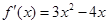 ,点
,点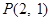 在曲线
在曲线 上.
上.
⑴ 当切点为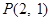 时,切线
时,切线 的斜率
的斜率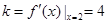 ,
,
∴ 的方程为
的方程为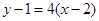 ,即
,即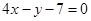 . ……………………5分
. ……………………5分
⑵当切点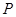 不是切点时,设切点为
不是切点时,设切点为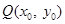
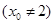 ,
,
切线 的斜率
的斜率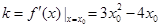 ,
,
∴ 的方程为
的方程为 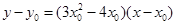 .
.
又点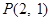 在
在 上,∴
上,∴ 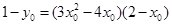 ,
,
∴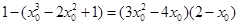 ,
,
∴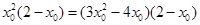 ,
,
∴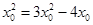 ,即
,即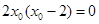 ,∴
,∴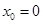 .
.
∴ 切线 的方程为
的方程为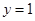
故所求切线 的方程为
的方程为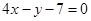 或
或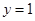 . ………………………………8分
. ………………………………8分
(Ⅲ)解: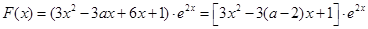 .
.
∴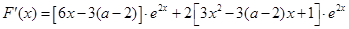
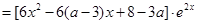
二次函数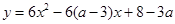 的判别式为
的判别式为
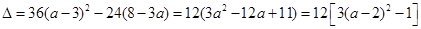 ,
,
令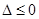 ,得:
,得: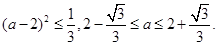
令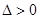 ,得
,得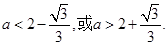 ………………………………10分
………………………………10分
∵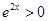 ,
,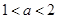 ,
,
∴当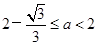 时,
时,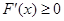 ,函数
,函数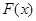 为单调递增,极值点个数为0;
为单调递增,极值点个数为0;
当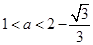 时,此时方程
时,此时方程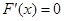 有两个不相等的实数根,根据极值点的定义,
有两个不相等的实数根,根据极值点的定义,
可知函数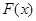 有两个极值点. ………………………………12分
有两个极值点. ………………………………12分
(1)因为函数
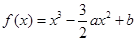 ,
,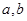 为实数,
为实数,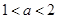 .求解导数。判定单调性和最值,结合
.求解导数。判定单调性和最值,结合 在区间
在区间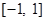 上的最小值、最大值分别为
上的最小值、最大值分别为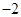 、1得到参数
、1得到参数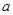 、
、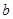 的值;
的值;(2)在(Ⅰ)的条件下,先求解导数值,然后得到经过点
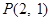 且与曲线
且与曲线 相切的直线
相切的直线 的方程;
的方程;(Ⅲ)设函数
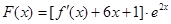 ,函数
,函数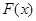 的极值点个数就是分析单调性来得到结论。
的极值点个数就是分析单调性来得到结论。解:(Ⅰ)由
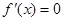 ,得
,得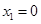 ,
,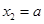 .
.∵
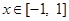 ,
,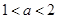 ,
,∴ 当
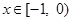 时,
时,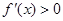 ,
, 递增;
递增;当
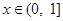 时,
时,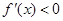 ,
, 递减.
递减.∴
 在区间
在区间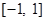 上的最大值为
上的最大值为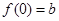 ,∴
,∴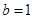 .……………………2分
.……………………2分又
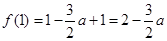 ,
,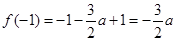 ,∴
,∴ 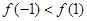 .
.由题意得
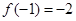 ,即
,即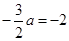 ,得
,得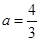 .
. 故
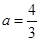 ,
,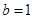 为所求. ………………………………4分
为所求. ………………………………4分(Ⅱ)解:由(1)得
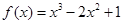 ,
,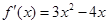 ,点
,点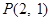 在曲线
在曲线 上.
上.⑴ 当切点为
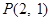 时,切线
时,切线 的斜率
的斜率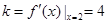 ,
,∴
 的方程为
的方程为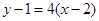 ,即
,即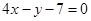 . ……………………5分
. ……………………5分⑵当切点
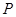 不是切点时,设切点为
不是切点时,设切点为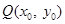
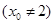 ,
,切线
 的斜率
的斜率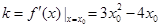 ,
,∴
 的方程为
的方程为 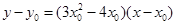 .
.又点
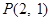 在
在 上,∴
上,∴ 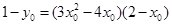 ,
,∴
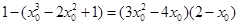 ,
,∴
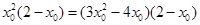 ,
,∴
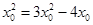 ,即
,即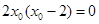 ,∴
,∴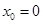 .
.∴ 切线
 的方程为
的方程为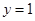
故所求切线
 的方程为
的方程为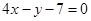 或
或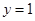 . ………………………………8分
. ………………………………8分(Ⅲ)解:
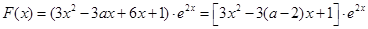 .
.∴
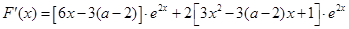
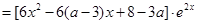
二次函数
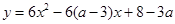 的判别式为
的判别式为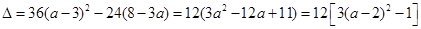 ,
,令
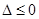 ,得:
,得: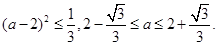
令
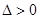 ,得
,得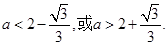 ………………………………10分
………………………………10分∵
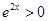 ,
,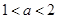 ,
,∴当
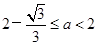 时,
时,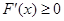 ,函数
,函数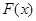 为单调递增,极值点个数为0;
为单调递增,极值点个数为0;当
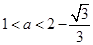 时,此时方程
时,此时方程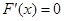 有两个不相等的实数根,根据极值点的定义,
有两个不相等的实数根,根据极值点的定义,可知函数
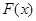 有两个极值点. ………………………………12分
有两个极值点. ………………………………12分
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
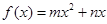 ,函数
,函数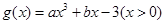 ,且有
,且有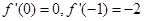 ,
,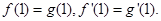
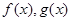 的解析式;
的解析式;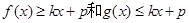 成立,若存在,求出k和p的值;若不存在,说明理由.
成立,若存在,求出k和p的值;若不存在,说明理由.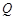 是曲线
是曲线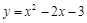 上的两点,且点
上的两点,且点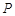 的横坐标是1,点
的横坐标是1,点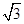 )x+
)x+ 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )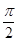 )
)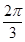 ,
,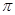 )
) 的图象经过点
的图象经过点 ,则它在
,则它在 点处的切线方程为
点处的切线方程为



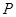 在曲线
在曲线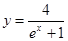 上,
上,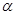 为曲线在点
为曲线在点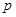 处的切线的倾斜角,则
处的切线的倾斜角,则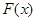 相同的方向移动,那么从位置
相同的方向移动,那么从位置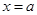 到
到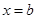 变力所做的功
变力所做的功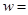 .
.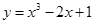 在点(1,0)处的切线方程为 ( )
在点(1,0)处的切线方程为 ( )