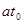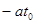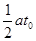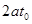题目内容
(本小题满分10分)求过点P(2,2)且与曲线y=x2相切的直线方程.
切线方程为y=(4± )x-(6±
)x-(6± ).
).
 )x-(6±
)x-(6± ).
).本试题主要是考查了导数的几何意义的运用。求解切线方程的问题。
根据已知条件,先求解函数的导数值,然后利用切点坐标为(x0,x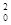 ),设出切线方程,把点P代入可知道x0
),设出切线方程,把点P代入可知道x0
从而得到结论。
解:y'=2x,过其上一点(x0,x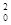 )的切线方程为
)的切线方程为
y-x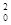 =2x0(x-x0),过P(2,2),故2-x
=2x0(x-x0),过P(2,2),故2-x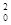 =2x0(2-x0)
=2x0(2-x0)
x0=2± . 故切线方程为y=(4±
. 故切线方程为y=(4± )x-(6±
)x-(6± ).
).
根据已知条件,先求解函数的导数值,然后利用切点坐标为(x0,x
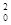 ),设出切线方程,把点P代入可知道x0
),设出切线方程,把点P代入可知道x0从而得到结论。
解:y'=2x,过其上一点(x0,x
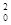 )的切线方程为
)的切线方程为y-x
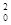 =2x0(x-x0),过P(2,2),故2-x
=2x0(x-x0),过P(2,2),故2-x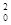 =2x0(2-x0)
=2x0(2-x0)x0=2±
 . 故切线方程为y=(4±
. 故切线方程为y=(4± )x-(6±
)x-(6± ).
).
练习册系列答案
相关题目
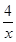 在点p(1,4)处的切线与直线l平行且距离为
在点p(1,4)处的切线与直线l平行且距离为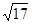 ,则直线l的方程为( )
,则直线l的方程为( )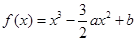 ,
,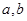 为实数,
为实数,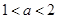 .
. 在区间
在区间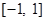 上的最小值、最大值分别为
上的最小值、最大值分别为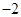 、1,求
、1,求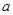 、
、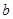 的值;
的值;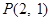 且与曲线
且与曲线 的方程;
的方程;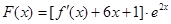 ,试判断函数
,试判断函数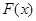 的极值点个数.
的极值点个数. 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为



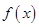 在
在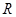 上的导函数为
上的导函数为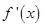 ,且
,且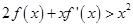 ,下面的不等式在
,下面的不等式在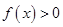
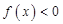

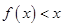
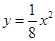 的一条切线的斜率为
的一条切线的斜率为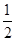 ,则切点的横坐标为( )
,则切点的横坐标为( )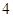
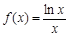 单调增区间是 ;
单调增区间是 ;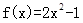 的图像上一点
的图像上一点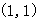 及邻近一点
及邻近一点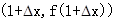 ,则
,则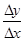 等于( )
等于( )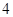

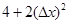
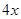
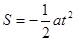 (
(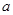 为常数),则该物体在
为常数),则该物体在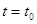 时刻的瞬时速度为( )
时刻的瞬时速度为( )