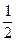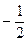题目内容
求函数y=sin2x+2sinxcosx+3cos2x的最小值,并写出使函数y取最小值的x的集合.
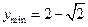 , y取最小值的x的集合为
, y取最小值的x的集合为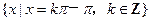 .
.解:y=sin2x+2sinxcosx+3cos2x
=(sin2x+cos2x)+2sinxcosx+2cos2x ——1分
=1sin2x(1+cos2x) ——3分
=2+sin2x+cos2x
=2+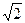 sin(2x+
sin(2x+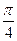 ). ——5分
). ——5分
当sin(2x+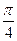 )=-1时y取得最小值2-
)=-1时y取得最小值2-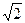 . ——6分
. ——6分
使y取最小值的x的集合为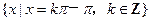 . ——8分
. ——8分
=(sin2x+cos2x)+2sinxcosx+2cos2x ——1分
=1sin2x(1+cos2x) ——3分
=2+sin2x+cos2x
=2+
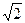 sin(2x+
sin(2x+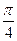 ). ——5分
). ——5分当sin(2x+
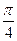 )=-1时y取得最小值2-
)=-1时y取得最小值2-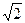 . ——6分
. ——6分使y取最小值的x的集合为
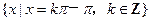 . ——8分
. ——8分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知
 的值; (2)设
的值; (2)设 ,求
,求 的值.
的值.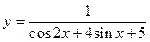 的值域是 .
的值域是 . 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 三个内角的正弦值,则( )
三个内角的正弦值,则( )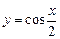 的最小正周期
的最小正周期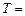 .
. 的定义域。
的定义域。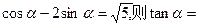 ( )
( )