题目内容
已知函数f（x）=
sin(
x-
)+2sin2(
x-
)（x∈R）．
（1）求函数f（x）的最小正周期；
（2）计算f（1）+f（2）+…+f（2008）．
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
（1）求函数f（x）的最小正周期；
（2）计算f（1）+f（2）+…+f（2008）．
由题意可得：函数f（x）=
sin(
x-
)+2sin2(
x-
)，
所以结合二倍角公式可得：
f（x）=
sin(
x-
)-cos(
x-
)+1
=2sin（
x-
）+1
（1）根据周期的计算公式可得：T=6，
所以函数f（x）的最小正周期为6．
（2）由题意可得：f（1）=1，f（2）=
+1，f（3）=
+1，f（4）=1，f（5）=-
+1，f（6）=-
+1，
所以f（1）+f（2）+f（3）+f（4）+f（5）+f（6）=6．
因为函数f（x）的最小正周期为6，
所以f（1）+f（2）+…+f（2008）=334×6+4+2
=2008+2
．
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
所以结合二倍角公式可得：
f（x）=
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
=2sin（
| π |
| 3 |
| π |
| 3 |
（1）根据周期的计算公式可得：T=6，
所以函数f（x）的最小正周期为6．
（2）由题意可得：f（1）=1，f（2）=
| 3 |
| 3 |
| 3 |
| 3 |
所以f（1）+f（2）+f（3）+f（4）+f（5）+f（6）=6．
因为函数f（x）的最小正周期为6，
所以f（1）+f（2）+…+f（2008）=334×6+4+2
| 3 |
| 3 |
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
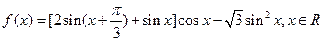
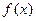的最小正周期；
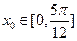，使不等式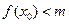
成立，求实数m的取值范围.
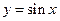在第一象限是增函数；②函数
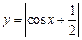的最小正周期是
；
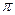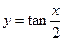的图像的对称中心是
；
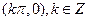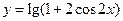的递减区间是[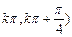
；
.
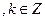