题目内容
△ 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知 成等比数列,
成等比数列,
求(1) 的值; (2)设
的值; (2)设 ,求
,求 的值.
的值.
 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知 成等比数列,
成等比数列,
求(1)
 的值; (2)设
的值; (2)设 ,求
,求 的值.
的值.(1)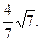 (2)3
(2)3
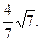 (2)3
(2)3(1)由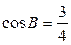 ,得
,得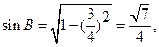
由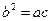 及正弦定理得
及正弦定理得 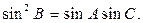
于是
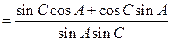
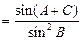
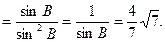
(2)由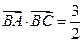 ,得
,得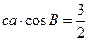 ,
,
由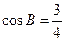 ,可得
,可得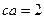 ,即
,即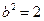 .
.
由余弦定理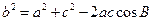 ,得
,得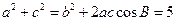 ,
,
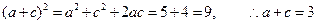 .
.
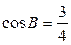 ,得
,得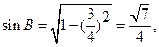
由
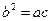 及正弦定理得
及正弦定理得 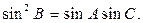
于是

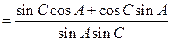
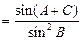
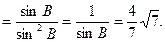
(2)由
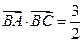 ,得
,得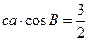 ,
, 由
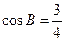 ,可得
,可得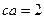 ,即
,即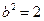 .
. 由余弦定理
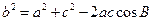 ,得
,得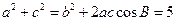 ,
,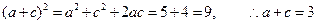 .
. 
练习册系列答案
相关题目
 ;(2)
;(2) 。
。 (米)是时间
(米)是时间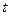 (0≤
(0≤
 的图像.
的图像.
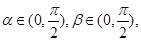 且
且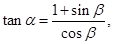 则( )
则( )



 ,且
,且 ,则 ( )
,则 ( )




 在第一象限,则在
在第一象限,则在 内
内 的取值范围是( )
的取值范围是( )


