题目内容
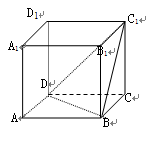
(本小题12分)已知空间四边形ABCD中,AC=AD,BC=BD,且E是CD的中点,F是BD的中点, (1)求证:BC∥平面AFE (2)平面ABE⊥平面ACD


解:设宾馆客房租金每间日租金提高x个10元,将有10x间客房空出,客房租金总收入为y.
由题意可得:y=(100+10x)(300-10x) (0≤x<30且x是整数) ……………..6
=100(-x2+20x+300) =-100(x-10)2+40000
当x=10时,ymax="40000 " ……………..10
因此每间租金100+10×10=200元时,客房租金总收入最高,日租金40000元。 …………..12
20、证明:(1)∵E,F分别是CD与BD的中点 ∴FE∥BC
∵ ∴ BC∥平面AFE ……………..6
∴ BC∥平面AFE ……………..6
(2)∵AC=AD,BC=BD,且E是CD的中点,F是BD的中点 ∴AE⊥DC BE⊥CD
∵ ∴CD⊥平面AEB
∴CD⊥平面AEB
∵ ∴平面ABE⊥平面ACD ……………….12
∴平面ABE⊥平面ACD ……………….12
由题意可得:y=(100+10x)(300-10x) (0≤x<30且x是整数) ……………..6
=100(-x2+20x+300) =-100(x-10)2+40000
当x=10时,ymax="40000 " ……………..10
因此每间租金100+10×10=200元时,客房租金总收入最高,日租金40000元。 …………..12
20、证明:(1)∵E,F分别是CD与BD的中点 ∴FE∥BC
∵
 ∴ BC∥平面AFE ……………..6
∴ BC∥平面AFE ……………..6(2)∵AC=AD,BC=BD,且E是CD的中点,F是BD的中点 ∴AE⊥DC BE⊥CD
∵
 ∴CD⊥平面AEB
∴CD⊥平面AEB∵
 ∴平面ABE⊥平面ACD ……………….12
∴平面ABE⊥平面ACD ……………….12略

练习册系列答案
相关题目
 的棱长为2,
的棱长为2, 分别是
分别是 的中点.
的中点.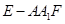 的体积;
的体积;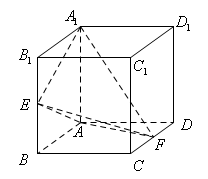
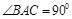 ,
,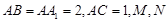 分别是
分别是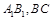 的中点。 (Ⅰ)证明:
的中点。 (Ⅰ)证明: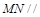 平面
平面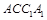 ;
;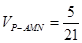 ,求
,求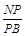 的值
的值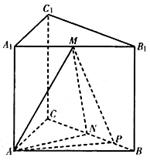
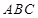 的边长为4,
的边长为4,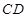 是
是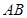 边上的高,
边上的高,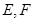 分别是
分别是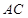
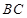 边的中点,现将△
边的中点,现将△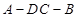 .
. 的位置关系,并说明理由;
的位置关系,并说明理由;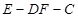 的余弦值;
的余弦值; ,使
,使 ?证明你的结论.
?证明你的结论.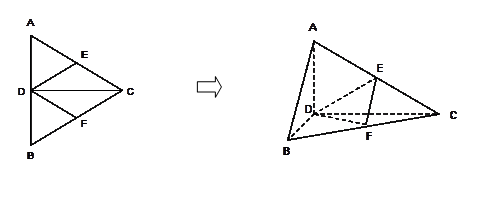
 、
、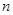 是不同的直线,
是不同的直线,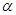 、
、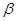 是不同的平面,有下列命题:
是不同的平面,有下列命题: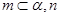 ∥
∥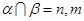 ∥
∥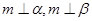 ,则
,则 个
个 个
个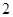 个
个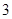 个
个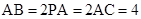 ,N为AB上一点且满足
,N为AB上一点且满足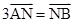 ,M,S分别为PB,BC的中点
,M,S分别为PB,BC的中点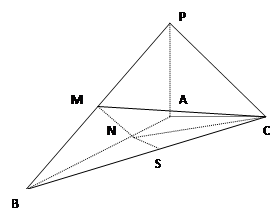
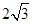 ,
,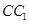 =
=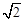 ,则二面角
,则二面角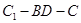 的大小为_______;
的大小为_______;