题目内容
f(x)=
x3-4x+4
(1)求函数的极值
(2)求函数在区间(-3,4)上的最大值与最小值.
| 1 |
| 3 |
(1)求函数的极值
(2)求函数在区间(-3,4)上的最大值与最小值.
(1)由f(x)=
x3-4x+4,得:f′(x)=x2-4.
由f′(x)=x2-4=0,得:x=-2,或x=2.
列表:
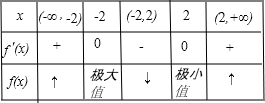
由表可知,函数f(x)的极大值为f(-2)=
×(-2)3-4×(-2)+4=
.
函数f(x)的极小值为f(2)=
×23-4×2+4=-
.
(2)因为f(-3)=
×(-3)3-4×(-3)+4=7.
f(4)=
×43-4×4+4=
.
又f(2)<f(-3)<f(-2),
f(2)<f(4)≤f(-2).
所以,函数f(x)在区间(-3,4)上的最大值为f(-2)=
.
最小值为f(2)=-
.
| 1 |
| 3 |
由f′(x)=x2-4=0,得:x=-2,或x=2.
列表:

由表可知,函数f(x)的极大值为f(-2)=
| 1 |
| 3 |
| 28 |
| 3 |
函数f(x)的极小值为f(2)=
| 1 |
| 3 |
| 4 |
| 3 |
(2)因为f(-3)=
| 1 |
| 3 |
f(4)=
| 1 |
| 3 |
| 28 |
| 3 |
又f(2)<f(-3)<f(-2),
f(2)<f(4)≤f(-2).
所以,函数f(x)在区间(-3,4)上的最大值为f(-2)=
| 28 |
| 3 |
最小值为f(2)=-
| 4 |
| 3 |

练习册系列答案
相关题目